Soma de Divisores

por gustavo7 Dom 28 Set 2014, 22:34

A soma de todos os divisores positivos de 1024 é igual a:

a)1025
b)1624
c)2047
d)2276
e)3072

Eu sei achar o número de divisores decompondo em números primos, mas eu não sei fazer a soma de todos os números positivos.

por **Elcioschin** Dom 28 Set 2014, 22:50

1024 = 2¹⁰

Divisores de 1024: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 ---> Basta somar

por BieelsZaitsev Dom 28 Set 2014, 22:57

Inicialmente é necessário decompor o 1024 para saber os números primos que o compõe.

2 | 1024
2 | 512
2 | 256
2 | 128
2 | 64
2 | 32
2 | 16
2 | 8
2 | 4
2 | 2
1

Se somar todos os valores da direita, os divisores, chega-se ao 2047.
--------------------

Mas existe um método mais elegante.

A considerar que existem 10 termos (n =10) em uma progressão geométrica de q = 2 e o primeiro termo valendo 2 (a1 = 2), utilizaremos a soma de uma progressão geométrica finita:

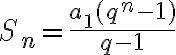
$Soma de Divisores Mimetex$

Sn = 2 . (2^10 - 1)/(2-1)
Sn = 2046

Como na progressão o 1 não entra, é necessário soma-lo depois:

2046 + 1 = R

R = 2047

Abraços e bons estudos!