Análise Combinatória

Alguém poderia me explicar o mecanismo dessa questão?
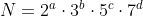Quantos divisores positivos tem o número ?

Resposta:

Olá, Emily.

Isso vem de um teorema da combinatória, que fala que o número de divisores naturais de um número qualquer, na sua forma fatorada, é:

\\ x = 2^a \cdot 3^b \cdot 5^c \dots \Leftrightarrow D(x) = (a+1) \cdot (b+1) \cdot (c+1)

Veja como ele é deduzido.

Suponha o número 25. Escrevamos seus divisores naturais:

1,5,25

Note que: 1 = 5⁰ e 25 = 5². O número de divisores é 2+1 = 3.

Peguemos agora o 36:

1,2,3,4,6,9,12,18,36

Note que: 1 = 2⁰=3⁰. E que 36 = 2²*3². O número de divisores é (2+1)*(2+1) = 9.

O que isso quer dizer? Quer dizer que na fatoração do 36, por exemplo, vemos que os seus divisores naturais são:

2⁰,2¹,2²,3⁰,3¹,3²,2*3,2*3²,2²*3²

Cada unidade no expoente representa um divisor; isso, aliado a permutação entre as possíveis bases, gera o produto (a+1)*(b+1)*(c+1) ..., no qual o +1 vem justamente do expoente 0, que fica omitido.

Por isso, o número de divisores naturais de \\ N = 2^a \cdot 3^b \cdot 5^c \cdot 7^d é (a+1) \cdot (b+1) \cdot (c+1) \cdot (d+1) .

Espero ter ajudado!

Att.,
Pedro

Muito admirada pela eficiência e agradecida pela generosidade 
Mas, veja, Pedro, quando eu fatorar um número para descobrir seus divisores naturais, eu tenho que essencialmente pegar o primeiro (no caso, o divisor universal -1-) e o último?


"Note que: 1 = 2⁰=3⁰. E que 36 = 2²*3². O número de divisores é (2+1)*(2+1) = 9."
Tal que se eu tentasse pelo número 49 ia seguir o mesmo caminho do número 25, supondo:
Divisores naturais de 49: 1, 7, 49
1 = 7⁰ e 49 = 7² de maneira que o número de divisores seria 2+1= 3...

Por outro lado, no entanto, pelo teorema da combinatória na fatoração de 36, por exemplo; 2⁰,2¹,2²,3⁰,3¹,3²,2*3,2*3²,2²*3²
eu observo somente a igualdade entre 3⁰ = 2⁰ = 1 (o inicial) e o último, 2²*3² = 36? Para então montar o (2+1)*(2+1)? 
Só uma luz nesse finalzinho pra tirar minha confusão no que consta a dedução 

Por nada,  .

Não é isso. É que o último é o próprio número.

5² = 25 e 2²*3² = 36. São a fatoração completa do número.

Pegue, por exemplo, 80.

Fatorando ele, temos:

80 | 2
40 | 2
20 | 2
10 | 2
  5 | 5
   1   --> 2⁴ . 5

Seu divisores serão, então:

2 ⁰ , 2¹,2²,2³, 2⁴ , 5 ⁰ , 5¹. 2*5,2²*5,2³*5,2 ⁴*5


O último já é o próprio número. Por isso, utilizamos ele para pegar o número de divisores.


D = (4+1)*(1+1) = 10


É isso.


Qualquer dúvida, chame!


Att.,
Pedro

Ah, entendi! Utilizamos o próprio número fatorado... precisou alguém me dizer pra enxergar isso   Obrigada 

Isso mesmo.



É um prazer ajudar.