Trigonometria II
2 participantes
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Trigonometria II
por L.Lawliet Sex 22 Ago 2014, 21:43
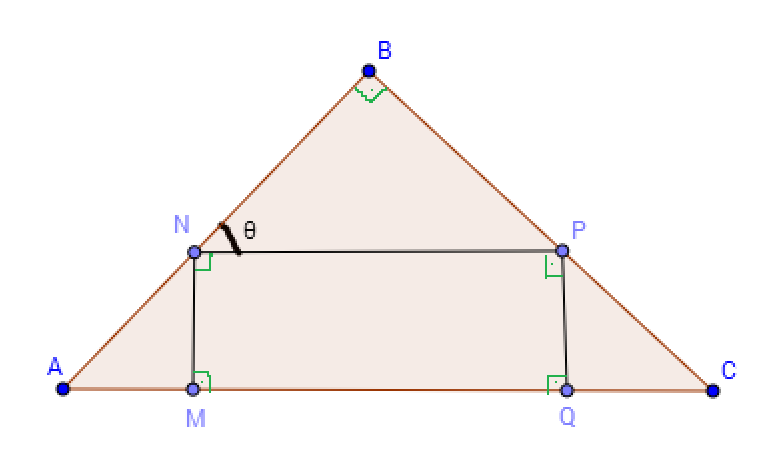
Na figura, calcule o minimo valor de E se MQ=2MN
https://i.gyazo.com/0a7cb81da54cbfd68f5c55b0cbbcbd5d.png
E = (Area de ∆ABC)/(Area de MNPQ)
A resposta é (2)
https://i.gyazo.com/0a7cb81da54cbfd68f5c55b0cbbcbd5d.png
E = (Area de ∆ABC)/(Area de MNPQ)
A resposta é (2)
L.Lawliet- Mestre Jedi
- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
Re: Trigonometria II
por Luck Sáb 23 Ago 2014, 22:53
N^BP = θ , N^PB = 90º-θ
NP // AC ∴ B^AC = θ , B^CA = 90º-θ
Sejam NM= PQ = x ; P = MQ = 2x , temos:
AN = x/senθ ; NB = 2xcosθ ; BP = 2xsenθ ; PC = x/cosθ
S(MNPQ) = x(2x) = 2x²
S(ABC) = (1/2)[(x/senθ) + 2xcosθ)][(2xsenθ + (x/cosθ) ]
S(ABC) = (1/2)x² [ (1/senθ) + 2cosθ)][2senθ + (1/cosθ)]
S(ABC) = (1/2)x²[ 2 + (1/senθcosθ) + 4senθcosθ + 2 ]
S(ABC) = (1/2)x²[ 4 + (2/sen2θ) + 2sen2θ ]
S(ABC)/S(MNPQ) = [4 + 2(sen2θ + (1/sen2θ) ) ] / 4 , com sen2θ > 0
M.A ≥ M.G :
(sen2θ + (1/sen2θ) ) / 2 ≥ √[(sen2θ)(1/sen2θ)]
sen2θ + (1/sen2θ) ≥ 2
Sendo a razão entre as áreas mínima, sen2θ + (1/sen2θ) = 2
S(ABC)/S(MNPQ) = (4 + 4)/4
S(ABC)/S(MNPQ) = 2
NP // AC ∴ B^AC = θ , B^CA = 90º-θ
Sejam NM= PQ = x ; P = MQ = 2x , temos:
AN = x/senθ ; NB = 2xcosθ ; BP = 2xsenθ ; PC = x/cosθ
S(MNPQ) = x(2x) = 2x²
S(ABC) = (1/2)[(x/senθ) + 2xcosθ)][(2xsenθ + (x/cosθ) ]
S(ABC) = (1/2)x² [ (1/senθ) + 2cosθ)][2senθ + (1/cosθ)]
S(ABC) = (1/2)x²[ 2 + (1/senθcosθ) + 4senθcosθ + 2 ]
S(ABC) = (1/2)x²[ 4 + (2/sen2θ) + 2sen2θ ]
S(ABC)/S(MNPQ) = [4 + 2(sen2θ + (1/sen2θ) ) ] / 4 , com sen2θ > 0
M.A ≥ M.G :
(sen2θ + (1/sen2θ) ) / 2 ≥ √[(sen2θ)(1/sen2θ)]
sen2θ + (1/sen2θ) ≥ 2
Sendo a razão entre as áreas mínima, sen2θ + (1/sen2θ) = 2
S(ABC)/S(MNPQ) = (4 + 4)/4
S(ABC)/S(MNPQ) = 2
Luck- Grupo
Velhos amigos do Fórum
- Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 32
Localização : RJ
L.Lawliet- Mestre Jedi
- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
Tópicos semelhantes» [Resolvido] TRIGONOMETRIA Parte I: Ajuda para resolver questões de trigonometria
» TRIGONOMETRIA: Ajuda para resolver questões de trigonometria
» TRIGONOMETRIA: Ajuda para resolver questões de trigonometria
» 23: trigonometria
» Trigonometria
» TRIGONOMETRIA: Ajuda para resolver questões de trigonometria
» TRIGONOMETRIA: Ajuda para resolver questões de trigonometria
» 23: trigonometria
» Trigonometria
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
