Círculos inscritos

No interior de um triângulo retângulo ABC temos três círculos, cada um deles tangente a dois lados do triângulo e aos outros dois círculos. Sanendo-se que os dois círculos tangentes à hipotenusa têm o mesmo raio R, determine o raio do terceiro círculo.



Resposta:

Seja A o ângulo reto e BC a hipotenusa
Sejam D e E os pontos de tangência das duas maiores com BC, F e G o das maiores com com os catetos AB e AC e M e N os da menos com os catetos AB e AC
Seja O, P os centros das duas maiores e Q o da menor
Sejam S o ponto de tangência das duas maiores e T, U os menor com as duas maiores
Seja r o raio da menor
 = 90º ---> ^B = ^C = 45º

Una BO, CP, AQ, OSP e PUQ e OTQ

OS = PS = R ----> OP = 2R ----> DE = 2R
OQ = OT + QT ---> OQ = R + r 
PQ = PU + QU ---> PQ = R + r -

MF² = (R + r)² - (R - r)² ---> MF² = 4.R.r ---> NG = MF = 2.√(R.r)

No triângulo retângulo BDO ---> O^BD = 45/2 = 22,5º

tg45º = 2.tg22,5º/(1 - tg²22,5º) ---> tg²22,5º + 2.tg22,5º - 1 = 0 --->

tg22,5º = [- 2 + - √(2² + 4)]/2 ---> tg22,5º = √2 - 1

tg22,5º = OD/BD --->  √2 - 1 = R/BD ----> OD =R.(√2 + 1)

BF = BD ---> BF = R.(√2 + 1)

BC = BD + DE + CE ---> BC = R.(√2 + 1) + 2R + R.(√2 + 1) ---> BC = R.2.(√2 + 2)

AB = AC = BC.cos45º ----> Calcule AB = AC

AB = AM + MF + BF ----> AB = r + 2.√(R.r) + R.(√2 + 1) ---> Calcule r

Élcio, creio ter havido pequena distração aqui:

AB = AM + MF + BF ----> AB = r + (R + r) + R.( √2 + 1) ---> Calcule r

O quadrilátero MFOQ é, na verdade, um trapézio retângulo; portanto MF não é paralelo a OQ, logo, MF≠R+r.

MF² = (R+r)² - (R-r)² -----> MF² = R² + 2Rr + r² - R² + 2Rr - r² ----> MF² = 4Rr
MF = 2√(Rr) -----> agora podemos calcular r.

Perfeito Medeiros. Foi distração minha. Obrigado pela checagem.

Elcio, como voce descobriu que o triangulo é isoceles? Além disso, porque MF seria igual a OQ?

De qual triângulo você fala?

Se for o triângulo maior ABC, pela própria simetria da figura isto fica claro: AB = AC

Se for o triângulo OPQ ---> 

OQ = OT + QT ---> OQ = R + r 
PQ = PU + QU ---> PQ = R + r

OQ = PQ ---> OPQ é isósceles

MF não é igual a OQ ---> O Medeiros já tinha mostrado isto e eu concordei
Veja a resposta do Medeiros.

Entendi. Obrigado pela explicação!

Você está certo ---> MF = 2.√(R.r) ---> Vou editar (em vermelho)


Eis uma figura para melhor entendimento:

Embora com solução já indicada pelo Élcio, a questão ainda não apresentou o valor final do raio menor e tem colegas com dificuldade em isolar e obtê-lo; por isto apresento a solução que obtive, que é semelhante a do Élcio.



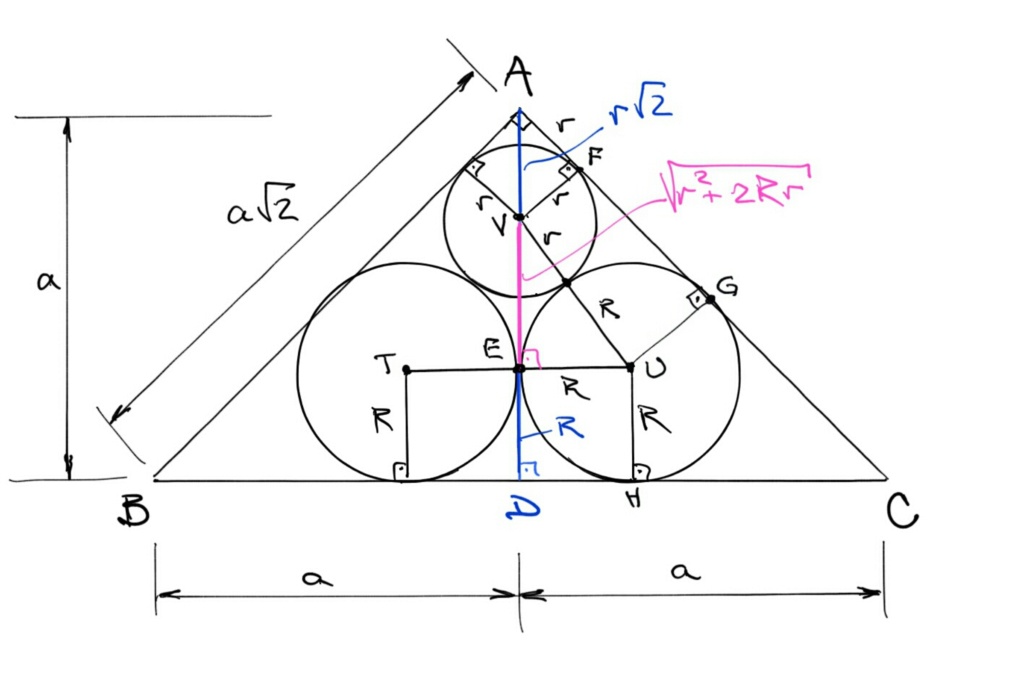
para que o ângulo reto se "equilibre" tangenciando as três circunferências, o triângulo retângulo ABC também deve ser isósceles, logo AB = AC. Neste caso, a altura AD, em relação à hipotenusa BC, o divide em outros dois triângulos retângulos isósceles.

Chamando BC = 2a, temos que AD = a e AB = AC = a√2.

AV = r.√2

considerando o triângulo VEU,
VE² = (R + r)² - R²  ----->  VE² = r² + 2.R.r  ----->  VE = √(r² + 2Rr)

ED = R

como,
AD = AV + VE + ED
\\a = r\sqrt{2} + \sqrt{r^2+2Rr} + R \;\;\;\;\; (1)

Vamos agora obter o valor para a constante "a" e, para isso, considerar o triângulo retângulo isósceles ADC. Ele tem uma circunferência inscrita de raio conhecido R. A área de ADC em função desse raio e do perímetro é dada por:
S_ADC = R.p ,
onde
S = a²/2
p = (a + a + a√2)/2  ---->  p = a.(2 + √2)/2
portanto, \frac{a^2}{2} = R.\frac{a.(2 + \sqrt{2})}{2} \to a = R.(2 + \sqrt{2}) \;\;\;\; (2)

(2) em (1) vem,
(e aqui termina a parte de geometria e o exercício fica puramente algébrico)
\\2R + R\sqrt{2} = r\sqrt{2} + \sqrt{r^2 + 2Rr} + R \\\\
R(1 + \sqrt{2}) - r\sqrt{2} = \sqrt{r^2 + 2Rr} \;\;\;\;\text{(elevando ao quadrado ambos os membros)} \\\\
R^2(1 + 2 + 2\sqrt{2}) + 2r^2 - 2Rr(\sqrt{2} + 2) = r^2 + 2Rr \\\\
r^2 - 2Rr(\sqrt{2} + 3) + (3 + 2\sqrt{2})R^2 = 0 \\\\
\Delta =4(2 + 9 + 6\sqrt{2})R^2 - 4(3 + 2\sqrt{2})R^2 \\\\
\Delta = 4(8 + 4\sqrt{2})R^2 \;\;\;\to\;\;\; \Delta = 16(2 + \sqrt{2})R^2 \\\\
r = \frac{2\sqrt{2} + 6 \pm 4\sqrt{2+\sqrt{2}}}{2}\cdot R \\\\
r = \left (\sqrt{2} + 3 \pm 2\sqrt{2 + \sqrt{2}} \right ).R^

evidentemente que r < R; portanto a soma entre parênteses deve ser um número menor do que a unidade e, assim, somente a raiz em que subtraímos o delta é aceitável. Então (vou aproveitar e separar aquele 3 em 2+1),
\\ r = \left ( \underset{a^2}{\underbrace{2 + \sqrt{2}}} + \underset{b^2}{\underbrace{1}} - \underset{2ab}{\underbrace{2.\sqrt{2+\sqrt{2}}}} \right ).R \;\; \to \;\; \boxed{\;\; r = \left (\sqrt{2+\sqrt{2}} - 1 \right )^2.R \;\;} \approx 0,72 R