Trigonometria.Qual é a altura da torre?

[size=24]Uma torre esta localizada em um terreno plano e horizontal. Sobre esse terno tomam-se dois pontos A e B distantes 126m do outro alinhados com base da torre.Do ponto A vai o ponto P mais alto da tore, sob um angulo de medida com o plano horizontal.Do ponto 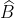ve-se P sob um angulo de medida 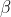com o plano horizontal.Calcule a altura da torre sabendo que sen. = 4/5 e sen. 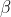= 12/13

Utilizando a relação Fundamenta da Trigonometria:
sen²α + cos²α = 1
(4/5)² + cos²α = 1
cos²α = 1 - 16/25 = (25 - 16)/25 = 9/25
cosα = 3/5

sen²α + cos²α = 1
(12/13)²β + cos²β = 1
cos²β = 1 - 144/169 = (169 - 144)/169 = 25/169
cosβ = 5/13

Encontrando a tgα:
tgα = senα/cosα
tgα = (4/5)/(3/5)
tgα = 4/3

Encontrando a tgβ:
tgβ = senβ/cosβ
tgβ = (12/13)/(5/13)
tgβ = 12/5



Encontrando a tgα no triângulo ACP:
tgα = (Cateto Oposto)/(Cateto Adjacente)
4/3 = h/(126 + x) --> h = 4(126 + x)/3 ----------(I)

Encontrando a tgβ no triângulo BCP:
tgβ = (Cateto Oposto)/(Cateto Adjacente)
12/5 = h/x --> h = 12x/5 ----------------------- (II)

Igualando (I) com (II):
4(126 + x)/3 = 12x/5
20(126 + x) = 36x
36x = 2520 + 20x
16x = 2520
x = 157,5 m

Substituindo x em (II):
h = 12.157,5/5
h = 1890/5
h = 378 m

obrigado por me ajuda vlw!!