polígonos .
+4
PedroCunha
victorbsb03
Berchades
LPavaNNN
8 participantes
Página 1 de 1
 polígonos .
polígonos .
Considere (P) um polígono regular de n lados. Suponha que os vértices de (P) determinem 2n triângulos, cujos lados, não são lados de (P). O valor de n é:
R:8
R:8
LPavaNNN- Grupo
Velhos amigos do Fórum
- Mensagens : 933
Data de inscrição : 22/04/2012
Idade : 30
Localização : Goiânia/GO Brasil
 Re: polígonos .
Re: polígonos .
Estou em dúvida também, alguém sabe?
Berchades- Padawan

- Mensagens : 75
Data de inscrição : 20/03/2012
Idade : 30
Localização : Sao paulo Sao paulo Brasil
 Re: polígonos .
Re: polígonos .
Somos 3 em dúvida então e a resposta no meu gabarito é 6 e não 8.
victorbsb03- Padawan

- Mensagens : 71
Data de inscrição : 29/03/2014
Idade : 28
Localização : Brasília - DF, Brasil
 Re: polígonos .
Re: polígonos .
Olá.
O número total de triângulos é Cn,3.
O número de triângulos que tem apenas um lado nos lados do polígono é n.
O número de triângulos que tem 2 lados nos lados do polígono é n*(n-4).
Então:
Cn,3 - n - n*(n-4) = 2n .:. Cn,3 - n - n² + 4n = 2n .:. Cn,3 = n²-n .:.
n*(n-1)*(n-2) = 6*n*(n-1), n diferente de 0: n² - 2n - n + 2 = 6n - 6 .:.
n² - 9n + 8 = 0 .:. n = (9 +- 7)/2 .:. n = 8 ou n = 1
n = 1 não serve, ficamos com n = 8.
Att.,
Pedro
O número total de triângulos é Cn,3.
O número de triângulos que tem apenas um lado nos lados do polígono é n.
O número de triângulos que tem 2 lados nos lados do polígono é n*(n-4).
Então:
Cn,3 - n - n*(n-4) = 2n .:. Cn,3 - n - n² + 4n = 2n .:. Cn,3 = n²-n .:.
n*(n-1)*(n-2) = 6*n*(n-1), n diferente de 0: n² - 2n - n + 2 = 6n - 6 .:.
n² - 9n + 8 = 0 .:. n = (9 +- 7)/2 .:. n = 8 ou n = 1
n = 1 não serve, ficamos com n = 8.
Att.,
Pedro

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Re: polígonos .
Re: polígonos .
Não sei se posso reabrir esse tópico caso não desculpe-me, mas realmente não queria postar essa dúvida de novo, poderia me explicar o motivo de triângulos com 2 lados serem iguais a n*(n-4)? Pelo que pensei seria triângulos com 1 lado que seria igual a n*(n-4), pois fixado um lado não posso usar os 2 vértices adjacentes e como já usei 2 vértices ao fixar um lado, logo ficaria (n-4) como são n lados:n*(n-4), mas isso seria para triângulos com 1 lado junto do polígono, para triângulos de 2 lados junto ao polígono..bem essa é uma das minhas dúvidas a princípio pensei em 3*n (pois podemos usar n vértices a partir dai abri em 3 casos, o vértice adjacente da direita que irá se ligar ao seu outro vértice adjacente, depois o mesmo para o vértice adjacente da esquerda que se ligará a seu vértice adjacente da esquerda e por fim escolhendo qualquer um dos vértices adjacentes e ligando este ao vértice oposto, formando um triângulo com o vértice escolhido e os dois adjacentes).Bem espero que eu tenha conseguido passar minha dúvida, e desculpe-me caso eu não possa reabrir algum tópico.Grato
allucardxxd- Iniciante
- Mensagens : 12
Data de inscrição : 20/03/2013
Idade : 31
Localização : santa maria
 Re: polígonos .
Re: polígonos .
Minha resolução estava parcialmente correta.
Faça um desenho para o caso onde n = 4 e n = 5 que você irá perceber:
2 lados no polígono: n
1 lado no polígono: n se for um quadrado e n*(n-4) para os restantes
Att.,
Pedro
Faça um desenho para o caso onde n = 4 e n = 5 que você irá perceber:
2 lados no polígono: n
1 lado no polígono: n se for um quadrado e n*(n-4) para os restantes
Att.,
Pedro

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Re: polígonos .
Re: polígonos .
Tendi obrigado 
allucardxxd- Iniciante
- Mensagens : 12
Data de inscrição : 20/03/2013
Idade : 31
Localização : santa maria
 Re: polígonos .
Re: polígonos .
Em relação a dois lados nas arestas podemos pensar da seguinte maneira: número de escolha de lados: n. Número de escolhas do lado vizinho ao escolhido anteriormente :2. Assim, para cada lado escolhido, formaremos dois triângulos. Mas, dois lados vizinhos possuem um triang em comum. Logo, todos os lados possuirão 1 x n triangs em comum. Total: 2n - n = n triangs com dois lados nas arestas adjacentes.
nandofab- Jedi

- Mensagens : 410
Data de inscrição : 25/07/2012
Idade : 29
Localização : Rio de Janeiro, RJ, Brasil
 Re: polígonos .
Re: polígonos .
Sobre essas 3 primeiras afirmaçõesPedroCunha escreveu:Olá.
O número total de triângulos é Cn,3.
O número de triângulos que tem apenas um lado nos lados do polígono é n.
O número de triângulos que tem 2 lados nos lados do polígono é n*(n-4).
Então:
Cn,3 - n - n*(n-4) = 2n .:. Cn,3 - n - n² + 4n = 2n .:. Cn,3 = n²-n .:.
n*(n-1)*(n-2) = 6*n*(n-1), n diferente de 0: n² - 2n - n + 2 = 6n - 6 .:.
n² - 9n + 8 = 0 .:. n = (9 +- 7)/2 .:. n = 8 ou n = 1
n = 1 não serve, ficamos com n = 8.
Att.,
Pedro
Isso tem em algum livro, apostila ou algo assim ou você as inferiu testando?
Legendcross- Recebeu o sabre de luz

- Mensagens : 163
Data de inscrição : 06/09/2015
Idade : 24
Localização : Brasil
Medeiros gosta desta mensagem
 resolução utilizando lemas de Kaplansky
resolução utilizando lemas de Kaplansky
Para formar os triângulos do enunciado é necessário escolher três vértices não adjacentes.Trata-se de um problema envolvendo o segundo lema de Kaplansky,pois se tem a escolha de elementos não-adjacentes em um ciclo(polígono).
Pelo lema:
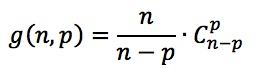
n é o número de vértices do polígono e p=3.
Dessa forma:
[latex]\frac{n}{n-3}\cdot \frac{(n-3)!}{3!(n-6)!}=2n[/latex]
Assim,n=8.
OBS:se não souber a fórmula do segundo lema de cabeça,uma vez que o assunto é raro de cair em provas,basta aplicar o primeiro lema duas vezes numerando os vértices de 1 a n.Em um primeiro caso,sem contar o vértice número um e no outro considerando este vértice e somando as possibilidades totais.
Pelo lema:
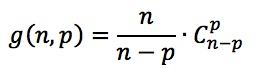
n é o número de vértices do polígono e p=3.
Dessa forma:
[latex]\frac{n}{n-3}\cdot \frac{(n-3)!}{3!(n-6)!}=2n[/latex]
Assim,n=8.
OBS:se não souber a fórmula do segundo lema de cabeça,uma vez que o assunto é raro de cair em provas,basta aplicar o primeiro lema duas vezes numerando os vértices de 1 a n.Em um primeiro caso,sem contar o vértice número um e no outro considerando este vértice e somando as possibilidades totais.
Última edição por augustohenrique02 em Sex 22 Out 2021, 22:53, editado 1 vez(es) (Motivo da edição : erro na escrita)

augustohenrique02- Iniciante
- Mensagens : 3
Data de inscrição : 24/09/2021
Idade : 20
Localização : São José dos Campos-SP
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












