Unicamp
4 participantes
Página 1 de 1
 Unicamp
Unicamp
O módulo da velocidade do som no ar é de aproximadamente 330m/s. Colocam-se dois alto falantes iguais, um defronte ao outro, distanciados 6,0m. Os alto-falantes são excitados simultaneamente por um mesmo amplificador com um sinal de frequencia de 220Hz.

Pergunta-se:
a) Qual é o comprimento da onda de som emitido pelos alto-falantes?
b) Em que pontos do eixo, entre os dois alto-falantes, o som tem intensidade máxima?
R-b): 0,75m; 1,5m; 2,25m; 3,0m; 3,75m; 4,5m e 5,25m do alto-falante da esquerda, além das posições onde se encontram os alto-falantes.
Alguém poderia me explicar com mais detalhes o porquê dessa resposta, já que ele pede os pontos de máxima intensidade (n par) pela fórmula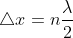 sendo assim os resultados que obtive foram apenas '' 0; 1,5; 3,0; 4,5; 6 ''.
sendo assim os resultados que obtive foram apenas '' 0; 1,5; 3,0; 4,5; 6 ''.

Pergunta-se:
a) Qual é o comprimento da onda de som emitido pelos alto-falantes?
b) Em que pontos do eixo, entre os dois alto-falantes, o som tem intensidade máxima?
R-b): 0,75m; 1,5m; 2,25m; 3,0m; 3,75m; 4,5m e 5,25m do alto-falante da esquerda, além das posições onde se encontram os alto-falantes.
Alguém poderia me explicar com mais detalhes o porquê dessa resposta, já que ele pede os pontos de máxima intensidade (n par) pela fórmula

igorgeoffroy- Iniciante
- Mensagens : 7
Data de inscrição : 10/07/2013
Idade : 29
Localização : Guarulhos, SP. Brasil.
 Re: Unicamp
Re: Unicamp
a) v = λ.f => λ = v/f => λ = 330/220 m = 1,5 m.
b) Como os alto-falantes são excitados simultaneamente, vem que as ondas lançadas por cada alto-falante estão em concordância de fase.
Sendo assim, ocorre interferência construtiva (I.C) para pontos que que distam d1 do alto falante da esquerda e d2 do alto falante da direita tal que ∆d = |d1 - d2| = (k.λ)/2, com 'k' par.
Logo, há interferência construtiva para os pontos que possuem ∆d = {0 m, 1,5 m, 3 m, 4,5 m, 6 m}.
Mas, da figura, d1 + d2 = 6 m.
Portanto, devemos resolver os seguintes sistemas :
1)
d1 + d2 = 6 m
|d1 - d2| = 0 m
________________
d1 = 3 m ; d2 = 3 m.
2)
d1 + d2 = 6 m
|d1 - d2| = 1,5 m
_________________
d1 = 3,75 m; d2 = 2,25 m ou d1 = 2,25 m e d2 = 3,75 m.
3)
d1 + d2 = 6 m
|d1 - d2| = 3 m
_________________
d1 = 1,5 m ; d2 = 4,5 m ou d1 = 4,5 m ; d2 = 1,5 m.
4)
d1 + d2 = 6 m
|d1 - d2| = 4,5 m
__________________
d1 = 5,25 m ; d2 = 0,75 m ou d1 = 0,75 m ; d2 = 5,25 m.
5)
d1 + d2 = 6 m
|d1 - d2| = 6 m
_________________
d1 = 6 m ; d2 = 0 m ou d1 = 0 m ; d2 = 6 m.
Assim, d1 (reitero que d1 é a distância do ponto onde ocorre interferência construtiva até o alto falante da esquerda) pode assumir os seguintes valores:
d1 = {0, 0,75 m, 1,5 m, 2,25 m, 3 m, 3,75 m, 4,5 m, 5,25 m}.
b) Como os alto-falantes são excitados simultaneamente, vem que as ondas lançadas por cada alto-falante estão em concordância de fase.
Sendo assim, ocorre interferência construtiva (I.C) para pontos que que distam d1 do alto falante da esquerda e d2 do alto falante da direita tal que ∆d = |d1 - d2| = (k.λ)/2, com 'k' par.
Logo, há interferência construtiva para os pontos que possuem ∆d = {0 m, 1,5 m, 3 m, 4,5 m, 6 m}.
Mas, da figura, d1 + d2 = 6 m.
Portanto, devemos resolver os seguintes sistemas :
1)
d1 + d2 = 6 m
|d1 - d2| = 0 m
________________
d1 = 3 m ; d2 = 3 m.
2)
d1 + d2 = 6 m
|d1 - d2| = 1,5 m
_________________
d1 = 3,75 m; d2 = 2,25 m ou d1 = 2,25 m e d2 = 3,75 m.
3)
d1 + d2 = 6 m
|d1 - d2| = 3 m
_________________
d1 = 1,5 m ; d2 = 4,5 m ou d1 = 4,5 m ; d2 = 1,5 m.
4)
d1 + d2 = 6 m
|d1 - d2| = 4,5 m
__________________
d1 = 5,25 m ; d2 = 0,75 m ou d1 = 0,75 m ; d2 = 5,25 m.
5)
d1 + d2 = 6 m
|d1 - d2| = 6 m
_________________
d1 = 6 m ; d2 = 0 m ou d1 = 0 m ; d2 = 6 m.
Assim, d1 (reitero que d1 é a distância do ponto onde ocorre interferência construtiva até o alto falante da esquerda) pode assumir os seguintes valores:
d1 = {0, 0,75 m, 1,5 m, 2,25 m, 3 m, 3,75 m, 4,5 m, 5,25 m}.
![JOAO [ITA]](https://2img.net/u/2713/85/25/58/avatars/20221-80.jpg)
JOAO [ITA]- Fera

- Mensagens : 866
Data de inscrição : 25/02/2012
Idade : 27
Localização : São José dos Campos,SP,Brasil
 Re: Unicamp
Re: Unicamp
Nossa cara agora entendi os resultados que obtive eram ∆d, e não os pontos (d1 ou d2) que distam do alto falante, faltava resolver os sistemas. Muito obrigado!

igorgeoffroy- Iniciante
- Mensagens : 7
Data de inscrição : 10/07/2013
Idade : 29
Localização : Guarulhos, SP. Brasil.
 Re: Unicamp
Re: Unicamp
Eu tenho uma dúvida teórica nessa questão.
Se as ondas estão em fase, não há interferencia construtiva ao logo de toda a onda? Afinal, as ondas possuem mesma frequencia e mesmo comprimento de onda.
Obrigada desde já
Se as ondas estão em fase, não há interferencia construtiva ao logo de toda a onda? Afinal, as ondas possuem mesma frequencia e mesmo comprimento de onda.
Obrigada desde já
beatrizb- Padawan

- Mensagens : 78
Data de inscrição : 04/04/2013
Idade : 29
Localização : brasil
 Re: Unicamp
Re: Unicamp
JOAO [ITA] escreveu:a) v = λ.f => λ = v/f => λ = 330/220 m = 1,5 m.
b) Como os alto-falantes são excitados simultaneamente, vem que as ondas lançadas por cada alto-falante estão em concordância de fase.
Sendo assim, ocorre interferência construtiva (I.C) para pontos que que distam d1 do alto falante da esquerda e d2 do alto falante da direita tal que ∆d = |d1 - d2| = (k.λ)/2, com 'k' par.
Logo, há interferência construtiva para os pontos que possuem ∆d = {0 m, 1,5 m, 3 m, 4,5 m, 6 m}.
Mas, da figura, d1 + d2 = 6 m.
Portanto, devemos resolver os seguintes sistemas :
1)
d1 + d2 = 6 m
|d1 - d2| = 0 m
________________
d1 = 3 m ; d2 = 3 m.
2)
d1 + d2 = 6 m
|d1 - d2| = 1,5 m
_________________
d1 = 3,75 m; d2 = 2,25 m ou d1 = 2,25 m e d2 = 3,75 m.
3)
d1 + d2 = 6 m
|d1 - d2| = 3 m
_________________
d1 = 1,5 m ; d2 = 4,5 m ou d1 = 4,5 m ; d2 = 1,5 m.
4)
d1 + d2 = 6 m
|d1 - d2| = 4,5 m
__________________
d1 = 5,25 m ; d2 = 0,75 m ou d1 = 0,75 m ; d2 = 5,25 m.
5)
d1 + d2 = 6 m
|d1 - d2| = 6 m
_________________
d1 = 6 m ; d2 = 0 m ou d1 = 0 m ; d2 = 6 m.
Assim, d1 (reitero que d1 é a distância do ponto onde ocorre interferência construtiva até o alto falante da esquerda) pode assumir os seguintes valores:
d1 = {0, 0,75 m, 1,5 m, 2,25 m, 3 m, 3,75 m, 4,5 m, 5,25 m}.
Colegas, eu cheguei ao mesmo resultado do João, mas por esta linha de pensamento:
A intensidade será máxima quando a amplitude for máxima. Logo, isso ocorre nas regiões de encontro de cristas e vales. Como λ = 1,5, a distância entre os encontros de cristas e vales é λ/2 = 0,75
Então, encontrei esses pontos {0, 0,75 m, 1,5 m, 2,25 m, 3 m, 3,75 m, 4,5 m, 5,25 m} pela progressão aritmética de razão 0,75.
Alguém poderia me dizer se este meu raciocínio também é correto?
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













