Unicamp 92

(Unicamp
92) Sejam a1, a2,..., an,... e b1, b2,... bn,... duas progressões aritméticas.
Mostre que os pontos (aj,bj), j=1,2,..., estão em uma mesma reta.

Realmente não entendi essa questão, não entendo como provar que a razão entre as "razões" é constante mostra que os pontos pertencem à mesma reta.
Segui o raciocínio de que as duas P.A são duas retas, e quando X=1, elas dão a1 e b1. já que X=1 como um representa o primeiro termo de cada uma.
Então quando X=j, elas dão aj e bj.
Então sempre dois termos que tenham a mesma posição, estarão sempre numa reta com a tangente de 90º.
Coeficiente angular da reta:
m=aj-bj/j-j
Já que aj-bj/0 é indefinido, o que só acontece quando a tangente é de 90º ou 270º.
Supondo que a aj e bj, sejam termos de diferentes posições, aí somente a inclinações mudariam, e o coeficiente angular.
Mesmo que as razões sejam zero, as retas são constantes e os pontos continuam formando retas. O único modo de não formar reta é se b1=a1 e r1=r2. Porque aí aj e bj seriam o mesmo ponto.
aj-bj/j-j=m
aj=bj
0/0
Porém não sei explicar isso da forma mais matemática possível. 
E também faz todo sentido imaginar que dois pontos distintos sempre formam uma reta, lembro que havia algo sobre provar com matrizes e determinantes
e geometria analítica que dois pontos são sempre uma reta, mas ainda
não reestudei essa parte e estou meio perdido em como provar algebricamente isso.
Aquelas explicações já bastariam como uma resposta aceitável?
Agora, somente a nível de curiosidade, dois pontos com as mesmas coordenadas, podem ser considerados uma reta ou são eles considerados um ponto só?

Seja um exemplo simples

1ª PA ----> 1, 2, 3, 4 ..... ---> a1 = 1 ---> r = 1
2ª PA ----> 3, 5, 7, 9 ..... ---> a1 = 3 ---> r = 2

Pontos A(1, 3), B(2, 5), C(3, 7), D (4, 9)

Coeficiente angular de AB = (5 - 3)/(2 - 1) = 2
Coeficiente angular de BC = (7 - 5)/(3 - 2) = 2
Coeficiente angular de CD = (9 - 7)/(4 - 3) = 2

Note que o numerador do coeficiente angular é sempre 2 e o numerador é sempre 1

Logo é uma reta

Eu acho que não estou conseguindo realmente interpretar a questão, pois para mim são duas P.A e deve se provar que cada termo de posição  j de uma, forma uma reta com o termo de mesma posição da outra.
Considero cada P.A como sendo uma reta e como a razão sendo o coeficiente angular. E não entendo como mostrar que o coeficiente angular é constante prova que os dois pontos são pertencentes a uma mesma reta.
Mais ou menos desse jeito:



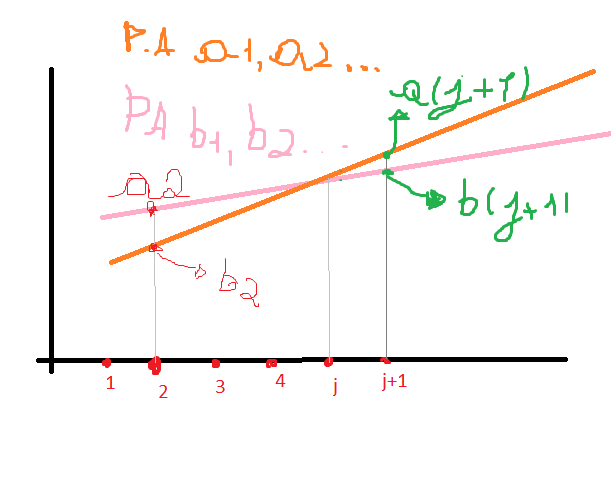
E o coeficiente angular das retas é aj-bj/j-j, o que dá uma indefinição, e aí a conclusão de que elas são retas inclinadas a 90º graus (desconsiderando a parte em que elas se interceptam que o coeficiente angular fica 0/0).
Ou a questão está pedindo que se prove que dois termos de uma mesma P.A pertencem a uma mesma reta?

São duas PA's cujos termos n ordenados formam pares ordenados. O que se deve é mostrar que esses pares ordenados estão sobre a mesma reta.

Mefistófeles,
este desenho procura esboçar a solução algébrica do Euclides.



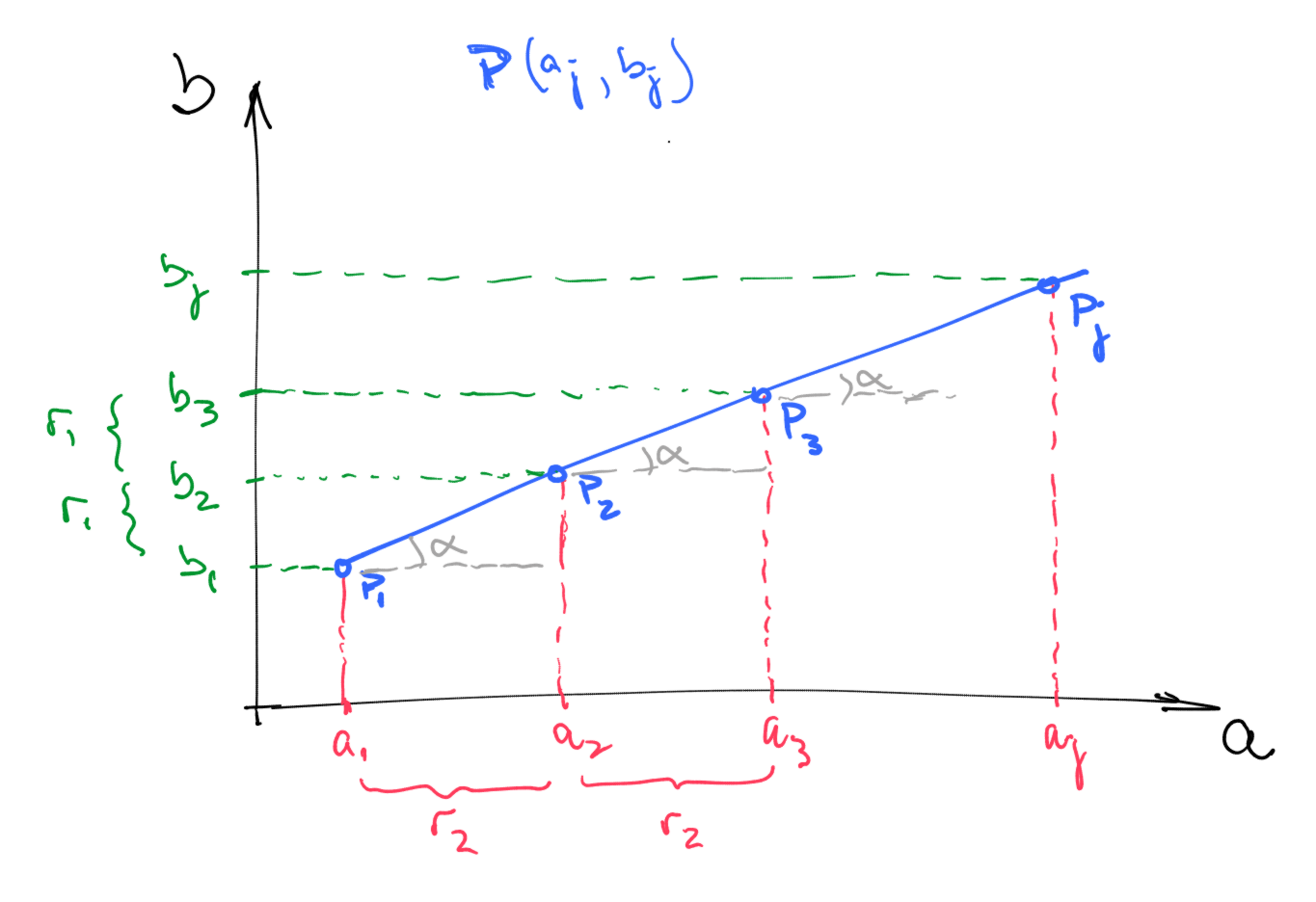
Existe apenas uma reta e não duas, como vc desenhou. Não é 'cada PA forma uma reta'; é 'os elementos consecutivos de cada PA que formam pares ordenados e tais pares estão sobre a mesma reta'.

Olá, colegas.

Vou dar minha contribuição:

Sejam os pontos . Suas coordenadas são:



Para eles estarem alinhados:



Abraços,
Pedro