Série de pagamentos
3 participantes
Página 1 de 1
 Série de pagamentos
Série de pagamentos
Uma dívida de 40.000 será liquidada em 12 prestações mensais e iguais, a 6% ao mês. Sabendo-se que a 1ª será paga daqui a 18 dias, determinar o valor das prestações.
R.: 4.661,16
Obrigado.
R.: 4.661,16
Obrigado.
jrfreitas- Iniciante
- Mensagens : 6
Data de inscrição : 23/12/2012
Idade : 53
Localização : São Paulo-Capital
 Re: Série de pagamentos
Re: Série de pagamentos
jrfreitas escreveu:Uma dívida de 40.000 será liquidada em 12 prestações mensais e iguais, a 6% ao mês. Sabendo-se que a 1ª será paga daqui a 18 dias, determinar o valor das prestações.
R.: 4.661,16
Obrigado.
1) Dados:
Vo' = 40 000
jm = 6% am = 0,06
xm = 1 + jm = 1,06 = x
P1 = P2 = ... = P12 = P
B12 = 0
2) Sabendo-se:
Vo.xⁿ + V1.xⁿˉ¹ + V2.xⁿˉ² + .... + Vn = Bn
Para coincidir o período mensal (30 dias), vamos levar Vo' = 40 000 para 12 dias atrás, transformando-o em Vo:
Vo = Vo'. x-¹²/³° = Vo' / (x¹²/³°)
Balanço em n=12: B12 = 0
x = 1,06
Vo' = 40 000
V1 = V2 + ... V12 = - P
3) Tem-se:
Vo.x¹² + V1.x¹¹ + V2.x¹° + .... + V12 = B12
Vo.x¹² - P.x¹¹ - P.x¹° - .... - P = 0
Vo.x¹² - P(x¹¹ + x¹° + .... + 1) = 0
Vo.x¹² = P(x¹¹ + x¹° + .... + 1)
Vo.x¹² = P (x¹² - 1) / (x - 1)
Vo.x¹²(x - 1) / (x¹² - 1) = P
Substituindo-se Vo:
Vo'. x-¹²/³°. x¹²(x - 1) / (x¹² - 1) = P
Vo'. x11,6(x - 1) / (x¹² - 1) = P
Substituindo-se os valores:
P = 40 000 . 1,0611,6 (1,06 - 1) / (1,06¹² - 1)
P ≈ 4 661,16
rihan- Estrela Dourada

- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
 Filminho da HP-12C resolvendo...
Filminho da HP-12C resolvendo...
Na calculadora ou na planilha é rapidinho...
Se você não tem uma HP-12C física (R$ 170,00 a R$ 300,00) ou virtual (emulador), é bom ter...
Link para emulador na web:http://epx.com.br/ctb/hp12c.php
Vamos para a HP-12C:
1) Limpar registradore financeiros e gerais:
f fin
f reg
2) Trazer Vo' para Vo, voltar 12 dias no tempo:
40000 ↑ 1.06 ↑ 12 ↑ 30 ↑ ÷ ↑ yx
3) Resolver o problema usando as funções da HP-12C:
Colocando o valor calculado no Presente Valor: PV
Colocando o número de períodos: 12 n
Idem para taxa de juro: 6 i
Idem para Futuro Valor: 0 FV
Obtendo a resposta do valor dos Pagamentos: PMT
4) Fim...
Se você não tem uma HP-12C física (R$ 170,00 a R$ 300,00) ou virtual (emulador), é bom ter...
Link para emulador na web:http://epx.com.br/ctb/hp12c.php
Vamos para a HP-12C:
1) Limpar registradore financeiros e gerais:
f fin
f reg
2) Trazer Vo' para Vo, voltar 12 dias no tempo:
40000 ↑ 1.06 ↑ 12 ↑ 30 ↑ ÷ ↑ yx
3) Resolver o problema usando as funções da HP-12C:
Colocando o valor calculado no Presente Valor: PV
Colocando o número de períodos: 12 n
Idem para taxa de juro: 6 i
Idem para Futuro Valor: 0 FV
Obtendo a resposta do valor dos Pagamentos: PMT
4) Fim...
rihan- Estrela Dourada

- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
 Re: Série de pagamentos
Re: Série de pagamentos
jrfreitas escreveu:Uma dívida de 40.000 será liquidada em 12 prestações mensais e iguais, a 6% ao mês. Sabendo-se que a 1ª será paga daqui a 18 dias, determinar o valor das prestações.
R.: 4.661,16
Obrigado.
Olá.
Usando a fórmula de série de pagamentos diferida: PV = PMT/(1+i)^k*[(1+i)^n-1]/[(1+i)^n*i]
Dados:
PV = 40000
i = 6% a.m. = 0,06 a.m.
n = 12 prestações mensais
k = 18/30 - 1 = - 0,4
PMT = ?
Colocando os dados na fórmula acima e calculando, vem:
40000 = PMT/1,06^(-0,4)*[1,06^12-1]/[1,06^12*0,06]
---->
40000 = PMT/0,97696196*1,01219647/0,12073179
---->
PMT = 40000*0,97696196/1,01219647*0,12073179
---->
PMT = 4.661,16
Um abraço.
jota-r- Grupo
Velhos amigos do Fórum
- Mensagens : 1668
Data de inscrição : 03/08/2009
Idade : 80
Localização : São Paulo - Capital
 Re: Série de pagamentos
Re: Série de pagamentos
Oi Jota-R !
Amigo Jota, creio que:
PV = PMT/(1+i)^k*[(1+i)^n-1]/[(1+i)^n*i]
É o mesma coisa que:
Vo'. x-¹²/³°. x¹²(x - 1) / (x¹² - 1) = P
Né ?
Abração !
Saudações Similares !
Amigo Jota, creio que:
PV = PMT/(1+i)^k*[(1+i)^n-1]/[(1+i)^n*i]
É o mesma coisa que:
Vo'. x-¹²/³°. x¹²(x - 1) / (x¹² - 1) = P
Né ?
Abração !
Saudações Similares !
rihan- Estrela Dourada

- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
 Re: Série de pagamentos
Re: Série de pagamentos
rihan escreveu:Oi Jota-R !
Amigo Jota, creio que:
PV = PMT/(1+i)^k*[(1+i)^n-1]/[(1+i)^n*i]
É o mesma coisa que:
Vo'. x-¹²/³°. x¹²(x - 1) / (x¹² - 1) = P
Né ?
Abração !
Saudações Similares !
Olá, amigo Rihan.
Concordo e, inclusive, acho sua solução mais elegante, pois você deduziu a fórmula a partir da teoria de P.G.
Contudo, "data vênia" (eh, mensalão), entendo que a minha é mais palatável para o público a que se destina (usuários de nível de ensino médio), até no que se refere à simbologia adotada, que é mais usual nos livros didáticos.
Grande abraço.
jota-r- Grupo
Velhos amigos do Fórum
- Mensagens : 1668
Data de inscrição : 03/08/2009
Idade : 80
Localização : São Paulo - Capital
 Re: Série de pagamentos
Re: Série de pagamentos
! !
!
Sei de cor algumas fórmulas, o que é útil para concursos.
Mas, para os que não querem ocupar o cérebro com coisas desnecessárias, basta conhecer a "terminologia financeira" e "saber de cor" a única fórmula necessária:
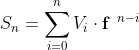
Então, por esse motivo, sempre parto dela.
Tem um post antigo meu, dividido em 5 partes:
https://pir2.forumeiros.com/t22503p15-financeira-valor-atual#77984
Caso queira saber mais sobre o que penso do péssimo ensino dessa disciplina, cá no Brasil, vá lá !
Abração !
Saudações reflexivas !
Sei de cor algumas fórmulas, o que é útil para concursos.
Mas, para os que não querem ocupar o cérebro com coisas desnecessárias, basta conhecer a "terminologia financeira" e "saber de cor" a única fórmula necessária:
Então, por esse motivo, sempre parto dela.
Tem um post antigo meu, dividido em 5 partes:
https://pir2.forumeiros.com/t22503p15-financeira-valor-atual#77984
Caso queira saber mais sobre o que penso do péssimo ensino dessa disciplina, cá no Brasil, vá lá !
Abração !
Saudações reflexivas !
rihan- Estrela Dourada

- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
 Re: Série de pagamentos
Re: Série de pagamentos
rihan escreveu:!!
Sei de cor algumas fórmulas, o que é útil para concursos.
Mas, para os que não querem ocupar o cérebro com coisas desnecessárias, basta conhecer a "terminologia financeira" e "saber de cor" a única fórmula necessária:
Então, por esse motivo, sempre parto dela.
Tem um post antigo meu, dividido em 5 partes:
https://pir2.forumeiros.com/t22503p15-financeira-valor-atual#77984
Caso queira saber mais sobre o que penso do péssimo ensino dessa disciplina, cá no Brasil, vá lá !
Abração !
Saudações reflexivas !
Olá, Rihan, boa tarde.
Comecei a analisar seu post e, pelo que já pude perceber, é um excelente trabalho, à altura de sua competência.
É público e notório que a qualidade do ensino no Brasil é deficiente, não apenas no tocante à matemática financeira, mas também quanto a todas as outras disciplinas e nos mais diversos níveis. Mas o que nós, simples mortais, podemos fazer para mudar essa realidade? Nada , né? Ciente dessa impossibilidade, adoto a máxima do dito popular que diz: "em terra de sapos, de cócoras com eles". E vou adotando a metodologia tupiniquim, até porque, qualquer tentativa de inovação que se queira introduzir nela é repelida por aqueles aos quais procuramos ajudar.
Sou usuário mais assíduo do fórum de matemática financeira do "Só Ensino" - http://www.soensino.com.br/foruns/viewforum.php?f=7&sid=9b7c84781c701165f5b0d935570fa934, que é muito visitado por alunos de cursos à distância, principalmente administração. A maioria é gente sem nenhuma base, incapaz até de diferenciar uma taxa nominal de uma taxa efetiva. Os livros-texto (virtuais) adotados por esses cursos são versões pioradas dos livros atuais de matemática financeira. E dá para perceber o nível medíocre dos professores e tutores que dão suporte aos alunos, de forma que não se pode fugir uma vírgula da metodologia disseminada entre esse pessoal. É uma verdadeira saia justa para quem, como nós, procura ajudar esse público. Por isso é que procuro, na medida do possível, manter-me fiel à cartilha deles.
Saudações justificadoras.
Grande abraço e ótima semana.
jota-r- Grupo
Velhos amigos do Fórum
- Mensagens : 1668
Data de inscrição : 03/08/2009
Idade : 80
Localização : São Paulo - Capital
 Re: Série de pagamentos
Re: Série de pagamentos
É isso aí !
Tudo de bom pra você também !
Abração ! !
!
Tudo de bom pra você também !
Abração !
rihan- Estrela Dourada

- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
 Tópicos semelhantes
Tópicos semelhantes» SÉRIE DE PAGAMENTOS UNIFORMES: CAPITALIZAÇÃO
» Série de pagamentos
» Série de pagamentos
» Série de pagamentos postecipados.
» SÉRIE DE PAGAMENTOS UNIFORMES: CAPITALIZAÇÃO
» Série de pagamentos
» Série de pagamentos
» Série de pagamentos postecipados.
» SÉRIE DE PAGAMENTOS UNIFORMES: CAPITALIZAÇÃO
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












