Área do triângulo através de integr

por Carlos Adriano de Sousa Dom 30 Dez 2012, 20:12

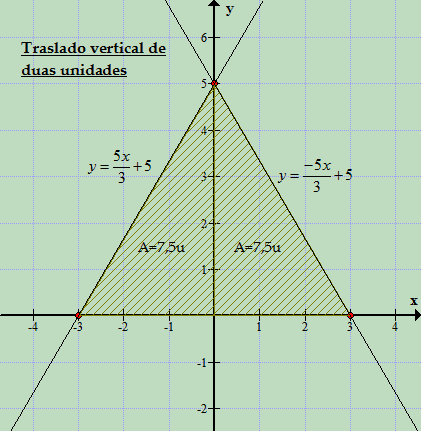
Pessoal boa noite tudo bem ? Estou com uma pequena dúvida em uma questão de cálculo, onde temos que calcular a área total, se formos calcular geometricamente teremos uma área igual a 15 u.a., mas eu demarquei algumas partes do triângulo para facilitar o cálculo, no entanto a parte que corresponde a cor azul não estou conseguindo encontrar uma forma de encontrar o valor da mesma, gostaria de saber em qual intervalo que posso começar, alguém poderia me ajudar ? Sei também que a área vermelha possui 5,4 u.a, a área verde possui 7,2 u.a e a área azul deveria possui em cada 1,2 u.a. totalizando 2,4 u.a, fazendo assim 15 u.a., fiz como f(x) - h(x), talvez eu tenha errado os intervalos, para facilitar também postarei as funções e detalhe a mesma deverá ser resolvida como integral:

f(x) = (5x/3) + 3
g(x) = (-5x/3) + 3
h(x) = -2

Área do triângulo através de integr Tringulo

Área do triângulo através de integr Tringulo

por **Euclides** Dom 30 Dez 2012, 20:42

Fazendo um traslado do triângulo duas unidades para cima:

Área do triângulo através de integr Resytri_zpsa1c3a903

integrando as novas funções

$A=\int_{-3}^{0}\left (\frac{5x}{3}+5 \right )dx+\int_{0}^{3}\left ( \frac{-5x}{3}+5 \right )dx$

por Carlos Adriano de Sousa Dom 30 Dez 2012, 22:57

Nossa Euclides eu nunca imaginaria isto, creio que a falta de visão seja por falta de prática, quando começar a praticar pra valer irei entender no momento, muito obrigado.

Euclides escreveu:Fazendo um traslado do triângulo duas unidades para cima:

integrando as novas funções

$A=\int_{-3}^{0}\left (\frac{5x}{3}+5 \right )dx+\int_{0}^{3}\left ( \frac{-5x}{3}+5 \right )dx$

por **Euclides** Dom 30 Dez 2012, 23:02

Pergunte a si mesmo:

- "eu saberia resolver, se o triângulo estivesse em outra posição?"

por Carlos Adriano de Sousa Dom 30 Dez 2012, 23:08

Euclides talvez se ele já estivesse na parte positiva do gráfico, conforme você colocou sim, mas também concordo com você em fazer a pergunta para eu mesmo e se por exemplo a figura estivesse virada para o lado, ou talvez de cabeça para baixo, realmente não sei e gostaria de fazer a seguinte ponderação, se puder elabore uma questão do gênero e me mande para que eu responda não o triângulo mais outra aí eu encontre outras dificuldades ou até mesmo outros tipos de visualizações, abraços e mais uma vez obrigado.

Euclides escreveu:Pergunte a si mesmo:

- "eu saberia resolver, se o triângulo estivesse em outra posição?"

por **Euclides** Dom 30 Dez 2012, 23:29

A questão abaixo pode ser resolvida através de uma integral definida simples:

"Encontre uma maneira de calcular o volume do sólido obtido pela revolução da parábola em torno do eixo horizontal, da origem até x=6."

Área do triângulo através de integr Trylong_zpscd6bbe77