Inequaçoes trigonométricas

por monicamanuela11 Sex 14 Dez 2012, 16:53

Alguém me ensina a resolver inequações? Já que não pode escrever ajuda, acho que pedir a alguém pra explicar deve poder. Um passo-a-passo de como resolver.

Determine os valores de x na inequação.

cos²x >= 2 ( senx + 1 )

por **ramonss** Sex 14 Dez 2012, 17:27

Primeiro, você deve desenvolver normalmente:

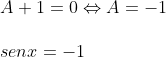
$Inequaçoes trigonométricas Gif$

Você vai chegar em alguma coisa. Nesse caso chegamos em uma equação de segundo grau na variável senx
Pra facilitar (desnecessário) nesse momento, vou chamar senx de A

$Inequaçoes trigonométricas Gif$

Um número ao quadrado só é menor ou igual a zero quando é igual a zero (é impossível ser menor).

$Inequaçoes trigonométricas Gif$

senx = -1
então
x = 3pi/2 + 2kpi

O seu exemplo não foi muito bom pq o resultado não caiu numa inequação e acabou caindo numa equação, Sad

Mas se tivesse caído, bastaria analisar o ciclo trigonométrico e pegar os valores que satisfizerem.

por **Matheus Vilaça** Sex 14 Dez 2012, 17:31

Pela Lei Fundamental da Trigonometria:
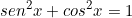
$\small \\sen^{2}x+cos^{2}x=1\\$
Logo:
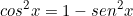
$\small \\cos^{2}x=1-sen^{2}x\\$

Substituindo na equação:
$\small \\1-sen^{2}x\geq 2senx+2\\ \\-sen^{2}x-2senx-1\geq 0\: \: \: \: \: \: \: (Multiplicando\: \:por\: \: -1)\\\\ {\color{Red} sen^{2}x+2senx+1\leq 0}\\$

Resolvendo a equação do Segundo Grau:
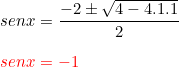
$\small \\senx=\frac{-2\pm \sqrt{4-4.1.1}}{2}\\\\ {\color{Red} senx=-1}$

De acordo com a equação temos que a mesma tem que dar um resultado menor ou igual a 0. Como ela possui concavidade para cima e toca somente 1 vez no eixo x, temos:
[img]

[/img]

Logo, pra qualquer valor do sen x ele terá valor positivo ou nulo (no caso de senx=-1). Assim,o único que satisfaz a condição dada na equação é senx=-1

Assim, a solução será:
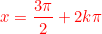
$\small {\color{Red} x=\frac{3\pi }{2}+2k\pi }$

por monicamanuela11 Sex 14 Dez 2012, 18:04

Obrigada!!

por monicamanuela11 Sex 14 Dez 2012, 20:55

Tem alguns exemplos que a gente muda o sinal da igualdade na resposta vocês sabem por quê?

por **Elcioschin** Sex 14 Dez 2012, 22:27

Geralmente é quando envolve bases de logaritmos entre 0 e 1

Outro caso é quando se trata de potência de bases entre 0 e 1

por monicamanuela11 Sex 14 Dez 2012, 23:10

Como assim?

por **Elcioschin** Sáb 15 Dez 2012, 10:28

Îsto é assunto para outro tópico. Vou mostrar apenas um exemplo:

(1/2)^x > (1/2)^4 ----> x < 4

Sugiro dar uma lida em qualquer livro, apostila ou mesmo na internet:

Logaritmos - Inequações logarítmicas

por mirellats Sáb 15 Dez 2012, 12:59

Olá Mônica. Acho q vc quer dizer no caso de:

-sen^2x - 2sen x - 1 > ou igual a zero

ao multiplicar por -1 ; vc deve inverter o símbolo:

sen^2 x + 2 sen x + 1 < ou igual a zero

vou dar um exemplo como explicação disso:

1<2 ook ? esta inequação está correta

agora pense comigo: multiplique ambos os lados por -1

-1 < -2 ---> isso é falso

para tornar a inequação verdadeira basta inverter o símbolo:

-1 > -2