Geometria analítica: determinar pontos da reta que pertencem ao plano

por acorreia Qui 24 maio 2012, 17:28

Seja C o conjunto de todos os pontos do plano euclidiano que distam 1 do ponto (x,y)=(2,1) e seja r a reta que passa pelos pontos (3,2) e (8,7).

Determine todos os pontos da reta r que pertencem ao conjunto C.
_________________________

Pessoal minhas respostas foram:

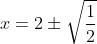
$x = 2 \pm \sqrt{\frac{1}{2}}$

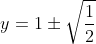
$y = 1 \pm \sqrt{\frac{1}{2}}$

Porém o professor disse que está errado, alguém pode me ajudar ?

Obrigado!

por **Euclides** Qui 24 maio 2012, 18:03

por **Elcioschin** Qui 24 maio 2012, 18:15

acorreia

Você postou sua questão de GA erradamente no fórum de Álgebra. Vou mudar.
Por favor, procure acertara nas próximas vezes.

Equação da reta r -----> y - 2 = [(7 - 2)/(8 - 3)]*(x - 3) ----> y = x - 1

POntos do plano equidistantes de P(2, 1) ----> circunferência com centro em P e raio R = 1:

(x - 2)² + (y - 1)² = 1² ----> (x - 2)² + [(x - 1) - 1]² = 1 -----> 2*(x - 2)² = 1 ----> (x - 2)² = 1/2 ----> x - 2 = ± \/2/2 ----> x = 2 ± \/2/2

y = x - 1 ----> y = (2 ± \/2/2) - 1 ----> y = 1 ± \/2/2

O Euclides colocou o centro da circunferência equivocado.

por **Euclides** Qui 24 maio 2012, 18:18

Obrigado Élcio!

por acorreia Qui 24 maio 2012, 18:20

Valeu Elcioschin!
Dei mole então, perdi a questão ;/

por **Elcioschin** Sex 25 maio 2012, 11:40

acorreia

Você ACERTOU a questão. Faltou somente racionalizar:

x = 2 ± \/(1/2) ----> x = 2 ± 1/\/2 ----> x = 2 ± \/2/2
y = 1 ± \/(1/2) ----> x = 1 ± 1/\/2 ----> x = 1 ± \/2/2