Plano dos complexos

No plano Argand-Gauss estão indicados um quadrado ABCD e os afixos dos números complexos Z0, Z1, Z2, Z3, Z4, e Z5.
Se o afixo do produto de Z0 por um dos outros cinco números complexos indicados é o centro da circun ferência inscrita no quadrado ABCD, então esse número complexo é: 



a) Z1 

b) Z2 

c) Z3 

d) Z4 

e) Z5

Spoiler:

Veja as minhas tentativas de resolução:    ----> a+bi=9i/4---> Z=9i/4



Complexo das coordenadas do centro: Z =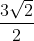    ; Z  , ou Z* =  

Z**=-1+i; ou Z =.(-1+i) = .



Outra tentativa de resolução: (-1+i).(a+bi)=---> Z=3/2i

** Complexo Z0 sem ser multiplicado pelo seu respectivo módulo
* Complexo das coordenadas do centro da circunferência sem ser multiplicado pelo seu respectivo módulo


Cheguei ao gabarito, após não multiplicar os números complexos indicados no plano pelos seus respectivos módulos... Fazendo a referida multiplicação, cheguei na resposta, z=9i/4, que não coincide com o gabarito... Porque tal multiplicação não deve ser realizada...

Em resumo pergunta-se qual dos 5 n⁰s complexos que multiplicado por Z0 fornece o centro da circunferência.

É mais fácil trabalhar com coordenadas polares porque simplificada as contas.

O centro da circunferência é dado por: \( Z_x = 1,5\sqrt{2}\angle225º \). O módulo 1,5√2 vem de Pitágoras e o ângulo é a bissetriz do 3⁰ quadrante. Precisamos descobrir qual produto fornece o afixo Zx

\( Z_0\times Z_1 = \sqrt{2}\angle135º\times 2\angle90º = 2\sqrt{2}\angle225º \) --> não serve, este é o vértice D do quadrado.

\( Z_0\times Z_2 = \sqrt{2}\angle135º\times 1,5\angle90º = 1,5\sqrt{2}\angle225º \) --> achamos

Portanto o complexo procurado é \( Z_2 = 1,5\angle90º = 0 + 1,5i = 1,5i \)

Claro, Medeiros... Então, a conclusão é que, quando os números complexos são estabelecidos no plano de Gaus, eles já estão na forma trigonométrica e nã se pode mais multiplicá-los pelos seus respectivos módulos...?!

Wadekly

acho que a culpa pela sua dúvida foi minha exposição inadequada. Como o Latex do fórum está inoperante, e portanto eu não conseguia indicar ângulos, tentei substituir por "cis" esperando que me entendessem. Fiz alterações na mensagem acima, veja se ficou mais claro.

Acontece o seguinte, quando devemos somar números complexos é mais fácil faze-los na forma retangular. Porém para multiplicar é mais fácil usar a forma polar pois basta multiplicar os módulos e somar os ângulos. Somente por isto usei a forma polar; ainda levando em conta que os módulos e os ângulos do gráfico são fáceis de identificar.

Sim... Você me fez vê onde erro, pois o que eu estava tentando fazer era chegar a forma trigonométria dos complexos partido já da forma trigonométrica... Por polar, você quer dizer: forma trigonométrica, certo...?!