Trapézio Isósceles

por quazxi04109090@gmail.com Qua 22 maio 2024, 15:54

Determine a diferença entre as medidas das bases de um trapézio isósceles circunscrito a um círculo de raio 3 cm, sabendo que a base média desse trapézio vale 6,5 cm.

a) 1,5 cm b) 2 cm c) 2,5 cm d) 4 cm e) 5 cm

por Lipo_f Qua 22 maio 2024, 16:34

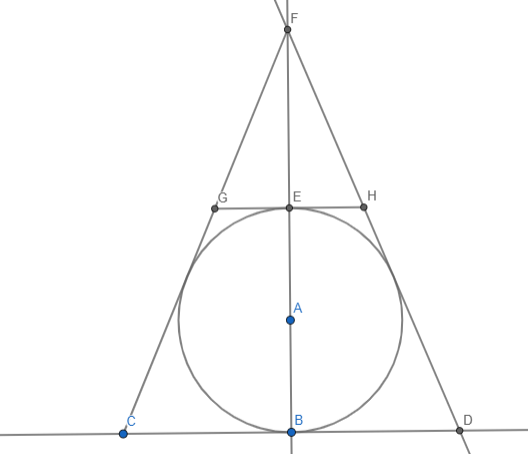
Construindo, você tem uma figura semelhante à figura abaixo. EB = 6 (um diâmetro). Do teorema de Pitot, B1 + B2 = 2L (L é o lado lateral) => L = 6.5. Baixe uma perpendicular por G (ou H), encontrando a base maior B1 em X. Segue que GXC é triângulo retângulo. Note que CX = 1/2 (B1 - B2) = D/2. Logo, (D/2)² + 6² = 6.5² <=> D²/4 = 6.25 => D² = 25 => D = 5cm

por quazxi04109090@gmail.com Qua 22 maio 2024, 17:10

É um trapézio isósceles Lipo_f. Não entendi.

por **Elcioschin** Qua 22 maio 2024, 17:51

por Lipo_f Qua 22 maio 2024, 19:01

quazxi04109090@gmail-com escreveu:É um trapézio isósceles Lipo_f. Não entendi.

O trapézio em questão é o HGCD. Se você prolongar os lados não paralelos, eles vão se encontrar em algum ponto, formando um triângulo. Eu ia fazer outra solução, as acabei tendo a ideia de Pitot no meio. Me esqueci de trocar a imagem rs. Só ignora a parte de cima, que a solução segue igual.

por Conteúdo patrocinado

Trapézio Isósceles

Trapézio Isósceles

Re: Trapézio Isósceles

Trapézio Isósceles

Re: Trapézio Isósceles

Re: Trapézio Isósceles

Re: Trapézio Isósceles

Um fórum livre e democrático.