Gráfico função modular

Seja [latex]g_{0}=\frac{\left | x+2 \right |-\left | x-2 \right |}{2}[/latex]
Faça o esboço do gráfico [latex]g_{1}=\frac{g_{0}(4x+6)+g_{0}(4x-6)}{2}[/latex]

mhope escreveu:Seja [latex]g_{0}=\frac{\left | x+2 \right |-\left | x-2 \right |}{2}[/latex]
Faça o esboço do gráfico [latex]g_{1}=\frac{g_{0}(4x+6)+g_{0}(4x-6)}{2}[/latex]

Boa noite, Mhope.
Para resolver problemas assim eu costumo transformar funções modulares em funções-sentença.

[latex]I)\: g_{0}= \frac{|x+2|-|x-2|}{2}\; e\; g_{1} = \frac{g_{0}(4x+6)+g_{0}(4x-6))}{2}[/latex]

[latex]II)\: g_{1} = \frac{g_{0}(4x+6+4x-6)}{2} = \frac{g_{0}(8x)}{2} = g_{0}(4x)[/latex]

[latex]III)\: g_{1} =  g_{0}(4x) \rightarrow g_{1} = \frac{4x(|x+2|-|x-2|)}{2} = 2x(|x+2|-|x-2|)[/latex]

[latex]IV)\: Utilizaremos\: a\: propriedade:|f(x)| = \left\{\begin{matrix} f(x)\: se\: f(x) \geq 0\\ ou\\ -f(x)\: se\: f(x) <0\\ \end{matrix}\right.[/latex]


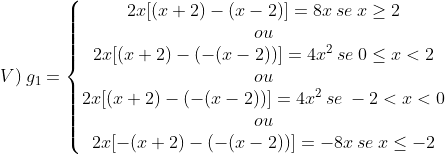
(Tive que colocar em PNG pois o LATEX estava bugado)
(Já escrevi tanta coisa que o fórum bugou, vou postar o gráfico logo abaixo)

Vou postar em link porque o fórum tá meio bugado pra mim.
https://i.servimg.com/u/f21/20/55/60/74/screen11.png