Pirâmide de base triangular
4 participantes
Página 1 de 1
 Pirâmide de base triangular
Pirâmide de base triangular
A base de uma pirâmide é um triângulo isósceles cuja base mede 30 cm e cujo ângulo do vértice é 120º. A altura da pirâmide mede 10 cm e passa pelo centro da circunferência circunscrita à base. Determine a medida da aresta lateral de pirâmide.
Gabarito: 20 cm
Gabarito: 20 cm

Zeroberto- Jedi

- Mensagens : 384
Data de inscrição : 14/12/2022
Idade : 19
Localização : Jaguariaíva - PR
 Re: Pirâmide de base triangular
Re: Pirâmide de base triangular
Como proposto no enunciado há duas medidas diferentes de aresta lateral.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Re: Pirâmide de base triangular
Re: Pirâmide de base triangular
Olá, Medeiros! Pior que o enunciado é assim mesmo, como está no livro.Medeiros escreveu:Como proposto no enunciado há duas medidas diferentes de aresta lateral.
Havia chego em 10√3 apenas aplicando uma lei dos cossenos com aquele ângulo; achei estranho não usar todas as outras informações que ele disse. Qual foi a resposta que você encontrou?

Zeroberto- Jedi

- Mensagens : 384
Data de inscrição : 14/12/2022
Idade : 19
Localização : Jaguariaíva - PR
 Re: Pirâmide de base triangular
Re: Pirâmide de base triangular
Última edição por Elcioschin em Seg 30 Out 2023, 19:13, editado 1 vez(es)

Elcioschin- Grande Mestre

- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Pirâmide de base triangular
Re: Pirâmide de base triangular
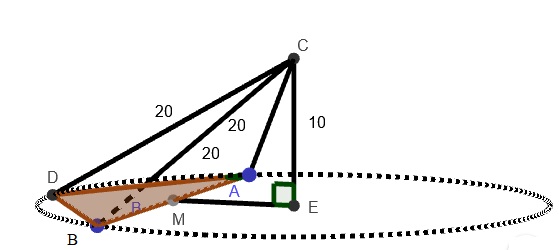
[latex]\\BM = \frac{30}{2}=15\\ ME = tg30 . 15 = 5\sqrt3 \implies R = 2.5\sqrt3=10\sqrt3\\ \triangle DEC = CD^2 = (10\sqrt3)^2+10^2 \therefore \boxed {CD = 20}\\ \triangle CEM: CM^2=10^2+(5\sqrt3)^2 \implies CM=5\sqrt7 \\ \triangle BCM:BC^2=BM^2+CM^2 \implies \boxed{BC = \sqrt{225+175}=20=AC} [/latex]
____________________________________________

_______________________________
"Ex nihilo nihil fit"
petras- Monitor

- Mensagens : 2117
Data de inscrição : 10/06/2016
Idade : 59
Localização : bragança, sp, brasil
 Re: Pirâmide de base triangular
Re: Pirâmide de base triangular
Elcioschin escreveu:O que vc calculou é apenas o valor dos lados iguais do triângulo da base:
Seja ABC o teriângulo da base com AB = AC = a, BC = 30 e A^BC = 120º
A^BC = A^CB = 30º
AB.cos30 + AC.cos30º = BC ---> L.√3/2 + L.√3/2 = 30 ---> AB = AC = L = 10.√3
Desenhe o triângulo ABC e inscreva nele uma circunferência de centro O que tangencia AB em M, AC em N e BC em P
OM = ON = OP = r
AP = AB.cosA^BC ---> AP = (10.√3).cos30º ---> AP = 15
OA.cos30º = OM ---> O.(√32/) = r ---> Calcule r
Continue e calcul o valor de r
Agora trace a pirâmide vértice V ---> trace AV, BV e CV ---> Note que BC = CV ≠ AV
Temos, portanto, dois tamanhos de arestas, conforme dito pelo Medeiros.
Élcio,creio que o enunciado quis dizer que o triângulo da base está circunscrito
____________________________________________

_______________________________
"Ex nihilo nihil fit"
petras- Monitor

- Mensagens : 2117
Data de inscrição : 10/06/2016
Idade : 59
Localização : bragança, sp, brasil
 Re: Pirâmide de base triangular
Re: Pirâmide de base triangular
Agora entendi perfeitamente! Interpretei bem mal aquele ângulo de 120º.
Medeiros, Elcio e Petras, muito obrigado pela ajuda!
Medeiros, Elcio e Petras, muito obrigado pela ajuda!

Zeroberto- Jedi

- Mensagens : 384
Data de inscrição : 14/12/2022
Idade : 19
Localização : Jaguariaíva - PR
 Re: Pirâmide de base triangular
Re: Pirâmide de base triangular
Consegui completar uma outra resolução que tinha pensado, mas que não foi para frente. O problema era aquele ângulo. Vou compartilhá-la para complementar o tópico:
Seja essa pirâmide de vértice D, base triangular ABC e aresta lateral l. Dado que A^BC é 120º e BC = 30. Pela lei dos senos:
\(\frac{30}{sen(\frac{2 \pi}{3})} = 2R \implies R = 10\sqrt3 \)
Olhando o triângulo ABC: seja O seu circuncentro. Do triângulo retângulo AOC:
\( (10)^2 + R^2 = l^2 \implies l^2 = 300 + 100 \therefore \boxed{l = 20 cm}\)
Apesar que olhando o desenho do Petras, essa minha resolução coincidiu com o resultado por pura sorte? Afinal, na resolução, indiretamente, acabei criando uma situação ideal e simétrica demais à generalidade do problema.
Seja essa pirâmide de vértice D, base triangular ABC e aresta lateral l. Dado que A^BC é 120º e BC = 30. Pela lei dos senos:
\(\frac{30}{sen(\frac{2 \pi}{3})} = 2R \implies R = 10\sqrt3 \)
Olhando o triângulo ABC: seja O seu circuncentro. Do triângulo retângulo AOC:
\( (10)^2 + R^2 = l^2 \implies l^2 = 300 + 100 \therefore \boxed{l = 20 cm}\)
Apesar que olhando o desenho do Petras, essa minha resolução coincidiu com o resultado por pura sorte? Afinal, na resolução, indiretamente, acabei criando uma situação ideal e simétrica demais à generalidade do problema.

Zeroberto- Jedi

- Mensagens : 384
Data de inscrição : 14/12/2022
Idade : 19
Localização : Jaguariaíva - PR
Medeiros gosta desta mensagem
 Re: Pirâmide de base triangular
Re: Pirâmide de base triangular
Tens razão petras: eu li errado e achei que a circunferência era inscrita.

Elcioschin- Grande Mestre

- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Pirâmide de base triangular
Re: Pirâmide de base triangular
Ze Roberto,Zeroberto escreveu:Olá, Medeiros! Pior que o enunciado é assim mesmo, como está no livro.Medeiros escreveu:Como proposto no enunciado há duas medidas diferentes de aresta lateral.
Havia chego em 10√3 apenas aplicando uma lei dos cossenos com aquele ângulo; achei estranho não usar todas as outras informações que ele disse. Qual foi a resposta que você encontrou?
eu não havia encontrado resposta alguma. Na ocasião li o enunciado pelo celular e no ônibus. Não atentei para o "circunscrita" e imaginei a pirâmide desenhada abaixo; fiquei contente que era uma pirâmide inclinada, com o pé da altura fora da base e por esse desenho mental achei que seriam duas arestas laterais diferentes. Mas nem pensei a respeito, deixei para resolver quando tivesse tempo e se ninguém ainda o houvesse feito. Claro que meu desenho não atende ao enunciado mas isto eu só veria se fosse resolver porque aí fica faltando o raio.
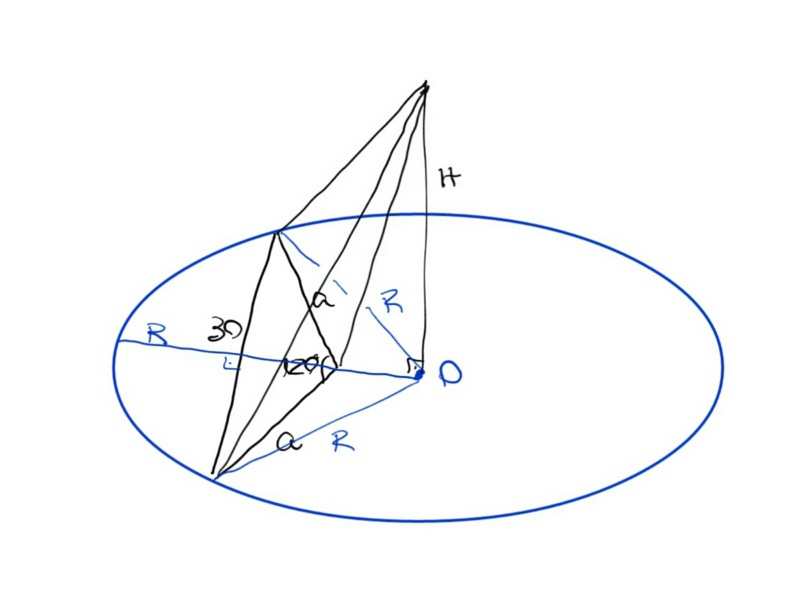
A propósito, Zé Roberto, achei a sua solução mais eficiente. Em duas linhas, de forma transparente, você chegou na resposta.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Zeroberto gosta desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» Pirâmide de base triangular
» Considere uma pirâmide triangular regular de base
» Pirâmide triangular
» Pirâmide triangular
» piramide triangular
» Considere uma pirâmide triangular regular de base
» Pirâmide triangular
» Pirâmide triangular
» piramide triangular
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












