Volume de Pirâmide

Considere o triângulo desenhado em uma folha de papel, junto com os eixos coordenados, cujos vértices são os pontos(0,0),(34,0) e (16,24).
Os vértices de seu triângulo médio são os pontos médios de seus lados. Uma pirâmide triangular é formada dobrando-se o triângulo ao longo dos lados de seu triângulo médio. Determine o volume dessa pirâmide.

Soluçao:

Eu fiz a imagem e calculei a base:
[latex]S_{base}=\dfrac{DE\cdot h}{2}=\dfrac{12\cdot 17}{12}=102[/latex]

Como calcular  a altura . Já vi uma resolução que ele considera o Vértice em (16,12,12), que daria uma altura de 12 e assim chegariamos a solução,  ou seja, ele girou o triangulo CDE 90 graus.  MAs como eu garanto que os outros vértices irão se encontrar nesse ponto? E por que necessariamente o ponto de encontro seria esse não outro?

Algumas informações adicionais:

Seja P(16, 0) ---> CP é altura de ABC ---> AP = 16 ---> BP = 18

BC² = BP² + CP² ---> BC² = 18² + 24² ---> BC = 30 ---> CE = BE = 15

AC² = AP² + CP² --> AC² = 16² + 18² --> AC = 2.√145 --> AD = CD = √145

EF² = (25 - 17)² + (12 - 0)² ---> EF = 4.√13

FD² = (17 - 8)² + (0 - 12)² ---> FD = 15

Considere o triângulo desenhado em uma folha de papel, junto com os eixos coordenados, cujos vértices são os pontos(0,0),(34,0) e (16,24).
Os vértices de seu triângulo médio são os pontos médios de seus lados. Uma pirâmide triangular é formada dobrando-se o triângulo ao longo dos lados de seu triângulo médio. Determine o volume dessa pirâmide.

Por Tales, os pontos médios determinam segmentos paralelos aos lados do triâng. ABC cujas medidas, pela semelhança de triângulos, valem a metade do respectivo lado paralelo.

Dobrando-se a ponta relativa ao vértice C sobre o segmento DE, se o fizermos até que encoste no plano do triângulo, obtemos o ponto C' reflexo de C em relação ao segmento DE; ou seja, o vértice C descreve um arco de circunferência cuja projeção sobre o plano do triângulo escursiona sobre a altura do triâng ABC em relação a este vértice. Portanto, tratando-se da pirâmide a ser construída, o lugar geométrico da projeção do vértice C é a altura h_C. Analogamente para os vértices A e B cujas projeções são as respectivas alturas. Logo se os três vértices devem se encontrar para formar o vértice de uma pirâmide eles obrigatoriamente deverão fazer isto num ponto cuja projeção é o ortocentro (H) do triâng. ABC.



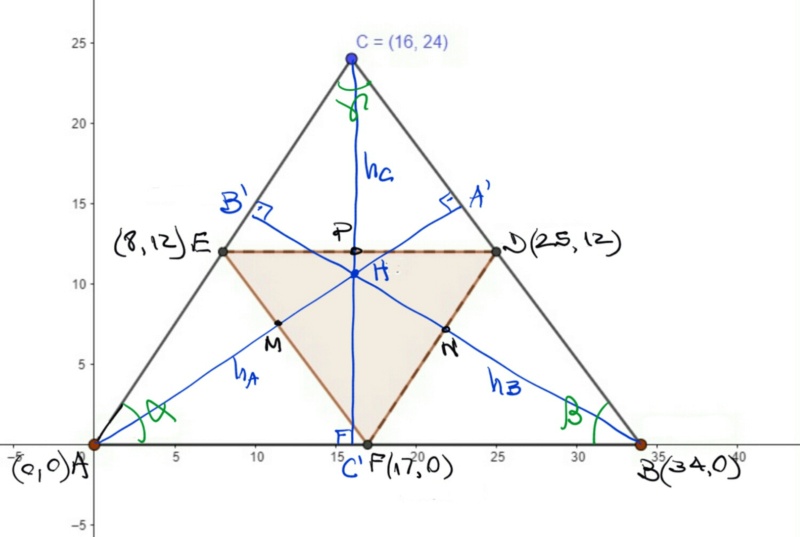
Precisamos das coordenadas do ortocentro H. O Morgado ensina que estas coordenadas são dadas pela média ponderada das coordenadas dos vértices usando como peso o valor das tangentes, ou seja, pela fórmula:

AB = 34
Pitágoras no ∆ACC'  --->  AC = 8√13 ≈ 28,8
Pitágoras no ∆BCC'  --->  BC = 30

h_C = 24
e pela comparação da área do triâng. ABC:
h_A = 136/5 = 27,2
h_B = 102√13/13 ≈ 28,3

AM = h_A/2 = 136/10 = 13,6
BN = h_B/2 = 51√13/13 ≈ 14,1
CP = h_C/2 = 12

∆ACC'  --->  tgα = 24/16 = 3/2
∆BCC'  --->  tgβ = 24/18 = 4/3
Pitágoras no ∆AA'C  --->  A'C² = AC² - h_A² = (8√13)² - (136/5)² = 2304/25  --->  A'C = 48/5 = 9,6
∆ACA'  ---> tgγ = 136/(5.A'C) = 136.5/(5.48)  --->   tgγ = 17/6 ≈ 2,83


aplicando na fórmula dada acima,


Se o ortocentro é H(16, 12) significa que ele fica sobre o segmento DE e coincide com o marcado ponto P (e não mais abaixo conforme desenhado). Então a face CDE da pirâmide forma um diedro a 90º com a base e portanto a altura da pirâmide é

Vamos verificar se é verdade que os vértices A e B encontrar-se-ão com C sobre o ortocentro H.  Para isto consideramos a pirâmide formada e aplicamos Pitágoras aos triângulos abaixo calculando o valor de h, que deverá ser o mesmo já encontrado (h=12). Precisamos antes obter as medidas de MH e NH.

Pitágoras no ∆AC'H  --->  AH = 20  ------------------>  MH = AH - AM = 20 - 136/10 = 32/5 = 6,4
Pitágoras no ∆BC'H  --->  BH = 6√3 ≈ 21,6  ----->  NH = BH - BN = 6√3 - 51√13/13 = 27√13/13 ≈7 ,5
e CP = 12  --->  PH = 0

Pitágoras no ∆AHM  --->  h² = AM² - MH² = √(13,6² - 6,4²)  --->  h = 12
PItágoras no ∆BHN  --->  h² = BN² - NH² = √[(51√13/13)² - (27√13/13)²]  --->  h = 12

Portanto fica confirmado que os três vértices do triângulo ABC encontram-se no mesmo ponto ao formar a pirâmide proposta pois todos resultam na mesma altura h para a pirâmide.

Volume da pirâmide

área da base -->  S = DE.PC/2 = 17.12/2 = 102
altura  --->  h = 12
volume  --->  V = (1/3).S.h = (1/3).102.12 = 102.4  ---->  V = 408

Muito bom..grato