Retas e plano

O plano π contém a reta r:x=-y=1-z e equidista dos pontos A=(1,0,0) e B=(0,1,0). Se os pontos A e B pertencem a semi espaços distintos em relação a π, então a abscissa do ponto de interseção de π com o eixo Ox é:
A) ⅓ B) ⅔ C) -⅓ D) -⅔ E) ¾

Não tenho o gabarito.
Perdão estar postando questões sem gabarito mas é pq eu tô corrigindo um simulado antigo e eu não tenho as respostas das questões.

O plano π contém a reta r:x=-y=1-z e equidista dos pontos A=(1,0,0) e B=(0,1,0). Se os pontos A e B pertencem a semi espaços distintos em relação a π, então a abscissa do ponto de interseção de π com o eixo Ox é:
A) ⅓ B) ⅔ C) -⅓ D) -⅔ E) ¾

Júlia, faz quase 50 anos que não brinco com isto mas vou tentar acertar, se é que a questão ainda lhe interessa.

O plano π equidista dos pontos A=(1,0,0) e B=(0,1,0) que estão um de cada lado do plano, então o ponto (M) médio de AB pertence ao plano.

O plano π contém a reta r: x = -y = 1-z. O vetor diretor da reta é u=(1, -1, -1) e um ponto dela é P(0, 0, 1), ambos também em π.

Consequentemente o vetor v=M-P também está contido em π ---> v = (1/2, 1/2, -1) = (1, 1, -2)


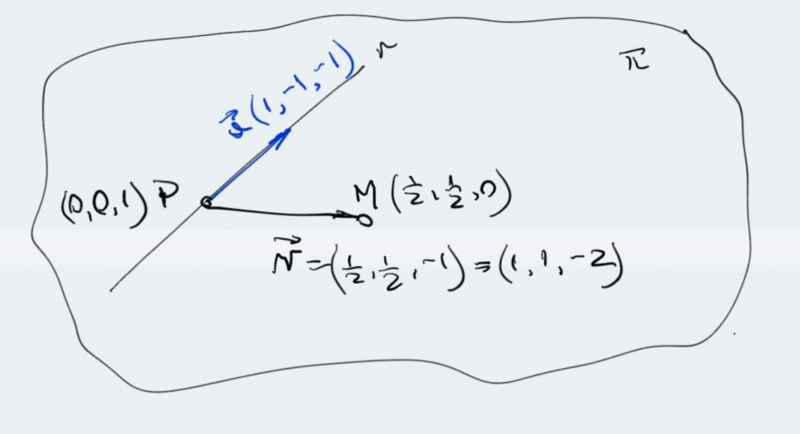
Temos dois vetores do plano π logo temos o vetor normal (n) do plano.

Portanto uma primeira equação normal do plano π é -----> 3x + y + 2z + k = 0
Obtemos o valor de k colocando o ponto P (que é do plano) na equação -----> 3.0 + 0 + 2.1 + k = 0 -----> k = -2
E então completamos a eq. do plano

A interseção de π com 0x implica em que tanto a ordenada quanto a cota do plano são zero, i.e., y = z = 0. Jogando esse dado na equação do plano: