Equação de curva.

por Bergamotinha OwO Sáb 16 Abr 2022, 01:46

Uma curva passa no ponto (0,5) e tem a propriedade de que a sua inclinação em todo ponto P é duas vezes a coordenada y de P.
Qual é a equação da curva?

Resp.: Sem gabarito.

Boa noite, amigos!
Como posso resolver essa? Sem ideias..
Vlww! cheers

por **qedpetrich** Sáb 16 Abr 2022, 02:13

Olá Bergamota;

A resolução não é minha, todos os créditos para o site Responde Aí.

Queremos achar a equação da curva y = f(x) que passa pelo ponto (0,5) e cuja inclinação seja dada por:

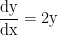
$Equação de curva. Png$

Assim, em cada ponto P(x , y), a inclinação será 2y. Essa é exatamente a equação do crescimento exponencial apresentada nessa seção, cuja solução é:

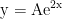
$Equação de curva. Png$

Como a curva deve passar no ponto (0 , 5), temos que:

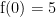
$Equação de curva. Png$

Assim:

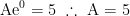
$Equação de curva. Png$

Portanto, a curva é dada por:

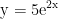
$Equação de curva. Png$

por **Giovana Martins** Sáb 16 Abr 2022, 02:51

[latex]\\\mathrm{Seja\ P(x,y). \ Do\ enunciado:\frac{dy}{dx}(x,y)=2y.\ Logo:}\\\\ \mathrm{\frac{dy}{y}=2dx\to \int \left ( \frac{1}{y} \right )dy=2\int dx\to ln(y)=2x+k,k=cte}\\\\ \mathrm{\therefore \ y=e^{2x+k}.\ Sendo\ y(0)=5\ \therefore\ 5=e^k\ \therefore\ k=ln(5)}\\\\ \mathrm{Ent\tilde{a}o:y=e^{2x+k}=y=e^{2x+ln(5)}=e^{2x}e^{ln(5)}\ \therefore\ y=5e^{2x}}[/latex]