Domínio de função

Olá amigos, estou com uma dúvida quanto ao Domínio dessa função:

[latex]f(x) = \sqrt{\frac{x-4}{x-13}}[/latex]

No caso, os cálculos apontam para:

 [latex]\left \{ x\in \mathbb{R} / x\leqslant 4 \vee x > 13 \right \}[/latex]

No entanto, acreditei que fosse possível visualizá-la como:

[latex]f(x) = \frac{\sqrt{x-4}}{\sqrt{x-13}}[/latex]

Porém, nesse sentido, o Domínio apresentado fica sendo:

[latex]\left \{ x\in \mathbb{R} / x > 13 \right \}[/latex]


Então...

Diante disso, parece que não é possível desenvolver a propriedade de radiciação:

[latex]\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}[/latex]

Por qual motivo há essa limitação? Onde está o erro nesse pensamento? Pois, para mim, o domínio deveria ser igual...

Saudações.

Isso acontece porque essa propriedade só é bem definida para a e b sendo números não negativos, visto que, quando são negativos, o numerador e o denominador podem resultar em raízes quadradas negativas, coisa que não existe no conjunto dos Reais. 

Quando você tem que 

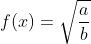, você deve analisar os casos para os quais a/b seja um número não negativo, ou seja:

a > 0 e b > 0 ou a < 0 e b < 0 ou a = 0 e b ≠ 0

Sabendo disso, temos que analisar o que foi citado:

i) x  - 4 > 0 ---> x > 4
x - 13 > 0 ---> x > 13

.:. x > 13

ii) x - 4 < 0 .:. x < 4
x - 13 < 0 .:. x < 13 

.:. x < 4

iii) x - 4 = 0 ---> x = 4
x - 13 ≠ 0 ---> x ≠ 13

.:. x = 4

Fazendo a união dos intervalos encontrados, temos:

S = {x ∈ R / (x ≤ 4) U (x > 13)}

Não sei se consegui ser muito claro ou usei o rigor matemático necessário mas posso tentar ajudá-lo se surgir alguma dúvida quanto a explicação.

Entendido! Ter essa persepção é fundamental para não cair no erro. Obrigado!