UEPG PSS III (2020/2021) POLINÔMIOS
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
UEPG PSS III (2020/2021) POLINÔMIOS
por thiagobelem Ter 30 Nov 2021, 20:47
Sabendo que a, b, c, d são as raízes da equação x^4 – 2x^3 – 9x^2 + 2x + 8 = 0, assinale o que for correto.
01) 1/a + 1/b + 1/c + 1/d = − 1/4 .
02) log (abcd) é um número primo.
2
04) a^2 + b^2 + c^2 + d^2 é um número múltiplo de dois.
08) ab + ac + ad + bc + bd + cd é um número positivo.
Gostaria de uma explicação detalhada da proposição número 04, se possível. Muito obrigado
01) 1/a + 1/b + 1/c + 1/d = − 1/4 .
02) log (abcd) é um número primo.
2
04) a^2 + b^2 + c^2 + d^2 é um número múltiplo de dois.
08) ab + ac + ad + bc + bd + cd é um número positivo.
Gostaria de uma explicação detalhada da proposição número 04, se possível. Muito obrigado
thiagobelem- Iniciante
- Mensagens : 23
Data de inscrição : 21/07/2020
Re: UEPG PSS III (2020/2021) POLINÔMIOS
por qedpetrich Ter 30 Nov 2021, 21:14
Olá thiagobelem;
Existem diversas formas de desenvolver a questão, pode recorrer a teoria polinomial e resolver por sistemas, optei pelo dispositivo prático de Briot-Ruffini, temos que para x = 1 uma solução, logo:
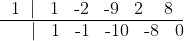
Ou seja, o polinômio pode ser reescrito sendo f(x) = x³-x²-10x-8. Testando para x = -1 vemos que também é raiz, aplicando novamente Briot-Ruffini, temos que:
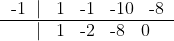
Ou seja, novamente podemos reescrever o polinômio sendo g(x) = x²-2x-8. Resolvendo a quadrática, temos que para g(x) = 0:
Portanto:
a = 1
b = -1
c = -2
d = 4
Da sua dúvida:
04) a² + b² + c² + d² é um número múltiplo de dois.
Conclui-se que trata-se de um número múltiplo de dois. Espero ter ajudado!
Existem diversas formas de desenvolver a questão, pode recorrer a teoria polinomial e resolver por sistemas, optei pelo dispositivo prático de Briot-Ruffini, temos que para x = 1 uma solução, logo:
Ou seja, o polinômio pode ser reescrito sendo f(x) = x³-x²-10x-8. Testando para x = -1 vemos que também é raiz, aplicando novamente Briot-Ruffini, temos que:
Ou seja, novamente podemos reescrever o polinômio sendo g(x) = x²-2x-8. Resolvendo a quadrática, temos que para g(x) = 0:
Portanto:
a = 1
b = -1
c = -2
d = 4
Da sua dúvida:
04) a² + b² + c² + d² é um número múltiplo de dois.
Conclui-se que trata-se de um número múltiplo de dois. Espero ter ajudado!
____________________________________________
Dê tempo ao
Lateralus Φ
qedpetrich- Monitor
- Mensagens : 2498
Data de inscrição : 05/07/2021
Idade : 24
Localização : Erechim - RS / Passo Fundo - RS
thiagobelem gosta desta mensagem
Re: UEPG PSS III (2020/2021) POLINÔMIOS
por Elcioschin Ter 30 Nov 2021, 21:57
Outro caminho, sem calcular as raízes: basta usar as Relações de Girard:
a + b + c + d = 2
a.b + a.c + a.d + b.c + b.d + c.d = - 9
a.b.c + a.b.d + a.c.d + b.c.d = - 2
a.b.c.d = 8
01) 1/a + 1/b + 1/c + 1/d = (a.b.c + a.b.d + a.c.d + b.c.d)/a.b.c.d = (-2)/8 = - 1/4 ---> correta
02) log2(a.b.c.d) = log2(8) = log2(2³) = 3 ---> correta
04) (a + b + c + d)² = a² + b² + c² + d² + 2.(a.b + a.c + a.d + b.c + b.d + c.d) --->
(2)² = a² + b² + c² + d² + 2.(-9) --> 4 = a² + b² + c² + d² - 18 ---> a² + b² + c² + d² = 22 ---> correta
08) a.b + a.c + a.d + b.c + b.d + c.d = - 9 ---> Falso
a + b + c + d = 2
a.b + a.c + a.d + b.c + b.d + c.d = - 9
a.b.c + a.b.d + a.c.d + b.c.d = - 2
a.b.c.d = 8
01) 1/a + 1/b + 1/c + 1/d = (a.b.c + a.b.d + a.c.d + b.c.d)/a.b.c.d = (-2)/8 = - 1/4 ---> correta
02) log2(a.b.c.d) = log2(8) = log2(2³) = 3 ---> correta
04) (a + b + c + d)² = a² + b² + c² + d² + 2.(a.b + a.c + a.d + b.c + b.d + c.d) --->
(2)² = a² + b² + c² + d² + 2.(-9) --> 4 = a² + b² + c² + d² - 18 ---> a² + b² + c² + d² = 22 ---> correta
08) a.b + a.c + a.d + b.c + b.d + c.d = - 9 ---> Falso
Elcioschin- Grande Mestre
- Mensagens : 73176
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
thiagobelem e qedpetrich gostam desta mensagem
Tópicos semelhantes» Polinômios - UEPG PSS III 2020/2021
» UEPG PSS III (2020/2021) CAMPO MAGNETICO
» AFA - 2020/2021
» Questão 30 do Colégio Tiradentes - 2020/2021
» uepg 2021 mecanica
» UEPG PSS III (2020/2021) CAMPO MAGNETICO
» AFA - 2020/2021
» Questão 30 do Colégio Tiradentes - 2020/2021
» uepg 2021 mecanica
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
