Logaritmos

por pedro_bello Sex 19 Nov 2021, 07:48

[latex]x^{\log_2x^2-\log_22x-2}+(x+2)^{\log_{(x+2)^2}4}=3[/latex]

por **qedpetrich** Sex 19 Nov 2021, 15:13

Olá pedro_bello;

Reescrevendo a expressão, temos que:

$Logaritmos Png$

É evidente que x > 1 como condição de logaritmando e desenvolvendo as raízes de x² - 2x + 2 = 0, logo:

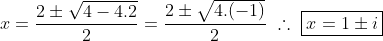
$Logaritmos Png.latex?x%20%3D%20%5Cfrac%7B2%5Cpm%20%5Csqrt%7B4-4.2%7D%7D%7B2%7D%20%3D%20%5Cfrac%7B2%5Cpm%20%5Csqrt%7B4$

Conclua o pensamento.

Creio que seja isso. Tem o gabarito?

por pedro_bello Sex 19 Nov 2021, 19:05

Parte dela está correta Petrich o gabarito é S={1,2,2^-3/4}

por **Elcioschin** Sex 19 Nov 2021, 19:50

pedro_bello

Você não está respeitando a Regra XI do fórum: sabia o gabarito e não postou, junto como enunciado.

Por favor leia/siga todas as Regras, para não correr o risco de ter suas postagens bloqueadas. E, se não souber o gabarito, escreva que não sabe.

por **qedpetrich** Sex 19 Nov 2021, 19:53

Pedro, você não está respeitando as regras do fórum, sabia o gabarito e não anexou ao corpo de texto. Tive uma interpretação errônea justamente pela falta de parênteses na mesma expressão. Interpretei como o -2 também fazendo parte do logaritmando, o que não é verdade, pois:

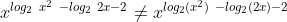
$Logaritmos Png$

Resolvendo da maneira "correta", temos que, primeiramente:

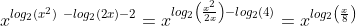
$Logaritmos Png$

Desenvolvendo temos que:

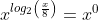
$Logaritmos Png$

Portanto uma solução trivial é que x = 1, pois:

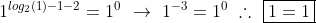
$Logaritmos Png$

Nossa outra solução é:

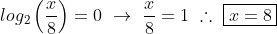
$Logaritmos Png$

Não cheguei nas mesmas soluções.. Como falei, um parênteses vai mudar todo o rumo da questão. Se puder esclarecer obrigado!

por pedro_bello Sex 19 Nov 2021, 20:09

Ehhh beleza então, eu realmente não sabia da regra do gabarito, não entendi por quê mais ok, não irá se repetir.

Petrich em relação ao parênteses, eu realmente não percebi que coloquei sem

[latex]x^{\log_2x^2-\log_2(2x)-2}[/latex]

aqui está a parte corrigida

por **qedpetrich** Sex 19 Nov 2021, 20:15

Bom, certamente o gabarito está errado, tomando x = 2, temos que:

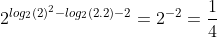
$Logaritmos Png.latex?2%5E%7Blog_2%282%29%5E2-log_2%282$

Dando sequência, logo:

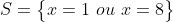
$Logaritmos Png$

As duas soluções são:

$Logaritmos Png$