Questão Pirâmide regular

por Tsuki Mikan Sex 24 Set 2021, 01:16

De um cubo de aresta medindo 6 cm apoiado sobre uma mesa, obtém-se os pontos B, C, D e E através dos centros de suas faces laterais e o ponto A através do centro de uma de suas bases. Assim, o volume da pirâmide ABCDE vale

A

6 cm³
B

12 cm³
C

18 cm³
D

36 cm³
E

54 cm³

por mao_sun Sex 24 Set 2021, 02:03

Não sei se está correto, mas espero que possa ajudar de alguma forma.

Prestando bem atenção nos dados da questão, conseguimos a seguinte imagem:

Todos os pontos B, C, D e E estão colocados no centro das laterais, e o A está no centro de uma das bases do cubo.

A distância entre cada ponto nas laterais até as arestas é igual a metade do tamanho do lado do cubo, assim, usando o ponto C e B como exemplos:

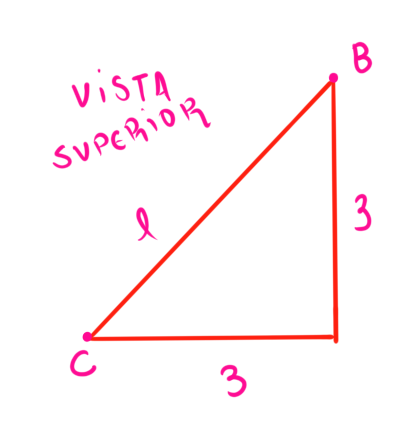
[latex]l^{2} = 3^{2} + 3^{2} = 2\cdot 3^{2} \therefore \boldsymbol{l = 3\sqrt{2}}[/latex]

A altura da pirâmide também será igual a metade do lado, pois o A está centralizado no centro e qualquer ponto (B, C, D, E) também.

Assim, sendo l o lado do quadrado da base da pirâmide e a altura igual a h, temos:

[latex]V = \frac{1}{3}\cdot B\cdot h \rightarrow V = \frac{1}{3}\cdot l^{2}\cdot h \rightarrow V = \frac{1}{3}\cdot (3\sqrt{2})^{2}\cdot 3 \\ \\ \boldsymbol{V = 18\: cm^{3}}[/latex]

Portanto, a resposta é a letra C.