(ITA - SP) - Trigonometria.

Bom dia amigos e amigas do fórum! Gostaria de uma confirmação a respeito dessa questão! Segue:

(ITA - SP) Sendo α e β os ângulos agudos de um triângulo retângulo, e sabendo que sen²(2β) - 2cos(2β) = 0, então o valor de senα é igual a:
A) √2 / 2
B) ⁴√2 / 2
C) ⁴√8 / 2
D) ⁴√8 / 4
E) zero

Resp.: Sem gabarito...

Então amigos, fiz da seguinte maneira, porém, não cheguei a nenhum resultado:

-> α + β = 90º
-> sen²(2β) - 2cos(2β) = 0
sen²(2β) = 2.cos(2β)
4.sen²β.cos²β = 2.cos²β - 1
4.cos²β(1 - cos²β) = 2.cos²β - 1
4.cos²β  - 4.cos⁴β = 2.cos²β - 1
4.cos⁴β - 2.cos²β - 1 = 0
-> Chamando cos²β = y...
4y² - 2y - 1 = 0
y = (1 + √5)/2 ou y = (1 - √5)/2

Logo, o cosβ pode ser o + ou - da raiz de y...
E como os ângulos são complementares, o cosβ = senα
Porém, não consigo ver aonde eu errei...
Quem puder me ajudar, agradeço desde já!!

Obs.: Caso alguém não tenha entendido a resolução, pontue que eu edito... Não sei usar o LATEX kkkk

sen²(2.B) - 2.cos(2.B) = 0

(2.senB.cosB)² - 2.(2.cos²B - 1) = 0

4.sen²B.cos²B - 4.cos²B + 2 = 0

4.(1 - cos²B).cos²B - 4.cos²B + 2 = 0

4.cos²B - 4.cos⁴B - 4.cos²B + 2 = 0 --->

4.cos⁴B = 2 ---> cos⁴B = 1/2 ---> cos⁴B = 8/16 ---> cos⁴B = 8/2⁴ ---> cosB = ∜8/2

senA = cosB ---> senA = ∜8/2

Fala, meu consagrado! Tudo certo?

Proponho uma solução diferente.







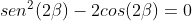
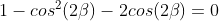
Mas:



Assim:









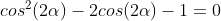
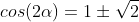
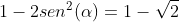
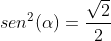
Por fim:



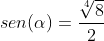
Espero ter ajudado! Grande Abraço!

Olá amigos!!
Antes de mais nada, mt obrigado pela ajuda! Estava tentando fazer essa questão desde ontem... mas sem sucesso.

Vi que, pela resolução do Elcio, tive um erro bobo kkkkk
Mas obrigado pela ajuda, tanto sua Elcio como sua tbm Foco!
Irei analisar sua resolução com carinho, uma resolução diferente mesmo!

Obrigado e abraços a ambos!