Dinâmica do movimento circular

por coqzieiro21 Sex Jul 30 2021, 19:49

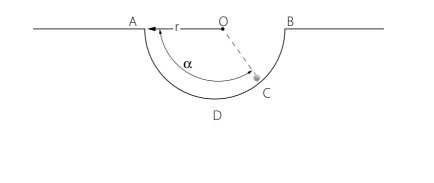
Uma pequena bola de massa m, inicialmente em A, desliza sobre uma superfície circular ADB sem atrito, conforme a figura. Demonstre que, quando a bola está no ponto C, a velocidade angular e a força exercida pela superfície são:

[latex]\omega = \sqrt{(2g.\sin \alpha )/r}[/latex]

[latex]F=3mg.\sin \alpha [/latex]

Olá pessoal, é a minha primeira vez por aqui, então peço desculpas se houver algum erro na formatação.

Att, Felipe.

por **Elcioschin** Sex Jul 30 2021, 20:04

h = diferença de nível entre C e A --->

h = r.sen(180º - a) ---> h = r.senα

Ep(A) = m.g.r
Ep(C) = m.g.(r - h) = m.g.(r - r.senα) ---> Ep(C) = m.g.r - m.g.r.senα

∆Ep = Ep(A) - Ep(C) ---> ∆Ep = m.g.r.senα

Ec(C) = m.V²/2 = m.(w.r)²/2 = m.w².r²/2

Ec(C) = ∆Ep ---> m.w².r²/2 = m.g.r.senα ---> w² = 2.g.senα/r --->

w = √(2.g.senα/r)

Tente completar; lembre-se que, sobre a bola atua uma força centrípeta, resultante da força peso e da reação normal da superfície.

por coqzieiro21 Sex Jul 30 2021, 20:44

Olá mestre, cheguei nessa resposta:

Ao decompor a força peso na direção radial ao movimento, podemos calcular a força normal (F) que o solo aplica sobre o corpo m:

Fcp = F - P.sen(α) ---> m.w².r = F - m.g.sen(α)

assim, F = m.w².r + m.g.sen(α)

sabendo que: w² = 2.g.senα/r , temos:

F = m.(2.g.senα/r).r + m.g.sen(α)

portanto, F = 3m.g.sin(α)

Usando a equação de torricelli eu encontrei a mesma resposta (admitindo que a velocidade inicial da bolinha é nula).

Muito obrigado.

Att, Felipe.

por Conteúdo patrocinado

Dinâmica do movimento circular

Dinâmica do movimento circular

Re: Dinâmica do movimento circular

Re: Dinâmica do movimento circular

Re: Dinâmica do movimento circular

Um fórum livre e democrático.