Discussão de sistemas
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Discussão de sistemas
Discussão de sistemas
A Soma dos valores de a que tornam o sistema possível e determinado é:
[latex] 3^(2x+1)x + y = 1 x + y = 0 (10.3^x.3)x + y = 1 R = 0 [/latex]
Olá, meus caros, Bom minha dúvida referente a esse exercício é a seguinte:
eu não poderia usar a seguinte relação
[latex]\frac{3^(2a+1)}{(10.3^x.3)} \neq 1[/latex]
para discutir esse sistema (2x2) ?? visto que a equação 2 é derivada da euquação 1 e 3

[latex] 3^(2x+1)x + y = 1 x + y = 0 (10.3^x.3)x + y = 1 R = 0 [/latex]
Olá, meus caros, Bom minha dúvida referente a esse exercício é a seguinte:
eu não poderia usar a seguinte relação
[latex]\frac{3^(2a+1)}{(10.3^x.3)} \neq 1[/latex]
para discutir esse sistema (2x2) ?? visto que a equação 2 é derivada da euquação 1 e 3

Última edição por Jvictors021 em Sáb 31 Jul 2021, 11:53, editado 2 vez(es)

Jvictors021- Estrela Dourada

- Mensagens : 1116
Data de inscrição : 02/07/2021
Idade : 21
Localização : Passa Quatro - MG
 Re: Discussão de sistemas
Re: Discussão de sistemas
Olá Jvictors021 
A imagem não está nítida e acredito que você se equivocou ao escrever o sistema. Ao meu ver, o sistema correto seria:
[latex]\\\left\{\begin{matrix} 3^{2a+1}x + y=1\\ x+y = 0\\ (10.3^a-3)x+y=1 \end{matrix}\right.[/latex]
De qualquer forma tentarei se o mais genérico possível, para que a solução seja a mesma para as variações do sistema.
A ideia é diminuir a equação 2 das equações 1 e 3, de forma que ficaremos com:
[latex]\\\left\{\begin{matrix} (3^{2a+1}-1)x =1\\ x+y = 0\\ (10.3^a-4)x=1 \end{matrix}\right.\\\\ \bullet(3^{2a+1}-1)\neq 0\rightarrow a\neq -\frac{1}{2}\\\\ \bullet(10.3^a-4)\neq 0 \rightarrow a\neq\log_3{(\frac{2}{5})}[/latex]
Agora que asseguramos que o coeficiente de x é diferente de zero, podemos passar ele para o outro lado dividindo:
[latex]\\\left\{\begin{matrix} x =\frac{1}{(3^{2a+1}-1)}\\ x+y = 0\\ x=\frac{1}{(10.3^a-4)} \end{matrix}\right.\xrightarrow{SPD}x =\frac{1}{(3^{2a+1}-1)}=\frac{1}{(10.3^a-4)}\\\\ \rightarrow 3^{2a+1}-1 = 10.3^a-4\\\\ \rightarrow 3.3^{2a}-10.3^{a}+3=0 \xrightarrow{3^a=z}3.z^2-10z+3=0\\\\ \rightarrow z=3^a=3\text{ ou }z=3^a=\frac{1}{3}\\\\ \rightarrow \boxed{a = 1\text{ ou }a=-1}[/latex]

A imagem não está nítida e acredito que você se equivocou ao escrever o sistema. Ao meu ver, o sistema correto seria:
[latex]\\\left\{\begin{matrix} 3^{2a+1}x + y=1\\ x+y = 0\\ (10.3^a-3)x+y=1 \end{matrix}\right.[/latex]
De qualquer forma tentarei se o mais genérico possível, para que a solução seja a mesma para as variações do sistema.
A ideia é diminuir a equação 2 das equações 1 e 3, de forma que ficaremos com:
[latex]\\\left\{\begin{matrix} (3^{2a+1}-1)x =1\\ x+y = 0\\ (10.3^a-4)x=1 \end{matrix}\right.\\\\ \bullet(3^{2a+1}-1)\neq 0\rightarrow a\neq -\frac{1}{2}\\\\ \bullet(10.3^a-4)\neq 0 \rightarrow a\neq\log_3{(\frac{2}{5})}[/latex]
Agora que asseguramos que o coeficiente de x é diferente de zero, podemos passar ele para o outro lado dividindo:
[latex]\\\left\{\begin{matrix} x =\frac{1}{(3^{2a+1}-1)}\\ x+y = 0\\ x=\frac{1}{(10.3^a-4)} \end{matrix}\right.\xrightarrow{SPD}x =\frac{1}{(3^{2a+1}-1)}=\frac{1}{(10.3^a-4)}\\\\ \rightarrow 3^{2a+1}-1 = 10.3^a-4\\\\ \rightarrow 3.3^{2a}-10.3^{a}+3=0 \xrightarrow{3^a=z}3.z^2-10z+3=0\\\\ \rightarrow z=3^a=3\text{ ou }z=3^a=\frac{1}{3}\\\\ \rightarrow \boxed{a = 1\text{ ou }a=-1}[/latex]

Victor011- Fera

- Mensagens : 663
Data de inscrição : 21/10/2015
Idade : 26
Localização : Rio de Janeiro, Brasil
Jvictors021 gosta desta mensagem
 Re: Discussão de sistemas
Re: Discussão de sistemas
Olá Victor me desculpe o erro de digitação, estou aprendendo a usar o LATEX, o sistema é o que você representou mesmo...Victor011 escreveu:Olá Jvictors021
A imagem não está nítida e acredito que você se equivocou ao escrever o sistema. Ao meu ver, o sistema correto seria:
[latex]\\\left\{\begin{matrix} 3^{2a+1}x + y=1\\ x+y = 0\\ (10.3^a-3)x+y=1 \end{matrix}\right.[/latex]
De qualquer forma tentarei se o mais genérico possível, para que a solução seja a mesma para as variações do sistema.
A ideia é diminuir a equação 2 das equações 1 e 3, de forma que ficaremos com:
[latex]\\\left\{\begin{matrix} (3^{2a+1}-1)x =1\\ x+y = 0\\ (10.3^a-4)x=1 \end{matrix}\right.\\\\ \bullet(3^{2a+1}-1)\neq 0\rightarrow a\neq -\frac{1}{2}\\\\ \bullet(10.3^a-4)\neq 0 \rightarrow a\neq\log_3{(\frac{2}{5})}[/latex]
Agora que asseguramos que o coeficiente de x é diferente de zero, podemos passar ele para o outro lado dividindo:
[latex]\\\left\{\begin{matrix} x =\frac{1}{(3^{2a+1}-1)}\\ x+y = 0\\ x=\frac{1}{(10.3^a-4)} \end{matrix}\right.\xrightarrow{SPD}x =\frac{1}{(3^{2a+1}-1)}=\frac{1}{(10.3^a-4)}\\\\ \rightarrow 3^{2a+1}-1 = 10.3^a-4\\\\ \rightarrow 3.3^{2a}-10.3^{a}+3=0 \xrightarrow{3^a=z}3.z^2-10z+3=0\\\\ \rightarrow z=3^a=3\text{ ou }z=3^a=\frac{1}{3}\\\\ \rightarrow \boxed{a = 1\text{ ou }a=-1}[/latex]
Entretanto minha dúvida é, se posso ou não utilizar a relação abaixo... Fico no aguardo da resposta. Um abraço!!
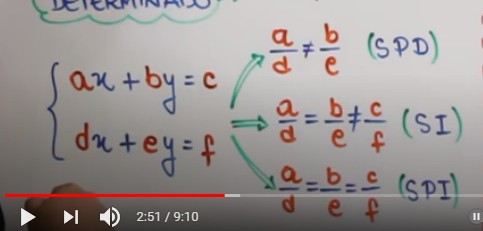

Jvictors021- Estrela Dourada

- Mensagens : 1116
Data de inscrição : 02/07/2021
Idade : 21
Localização : Passa Quatro - MG
 Re: Discussão de sistemas
Re: Discussão de sistemas
Essa decoreba que você está tentando usar é para sistemas com 2 incógnitas e 2 equações, enquanto que na questão temos 2 incógnitas e 3 equações. A única forma de conseguir usar essa decoreba seria reduzindo o número de equações da questão.
Para fazer isso, a ideia é pensar que em um SPD com 2 incógnitas, é obrigatório ter 2 equações. Logo, duas equações do sistema da questão tem que ser necessariamente iguais. Evidentemente, a única forma disso ocorrer seria a equação 1 ser igual a 3 (fazendo essa igualdade, já encontraríamos os valores de a e resolveríamos a questão, mas vamos prosseguir na sua dúvida).
Feito isso, reduzimos o sistema para duas equações, que podem ser as equações 1 e 2 ou 2 e 3.
Aplicando a sua decoreba nas equações 1 e 2:
[latex]\left\{\begin{matrix} 3^{2a+1}x+y=1\\ x+y=0 \end{matrix}\right.\;\rightarrow\;\frac{3^{2a+1}}{1}\neq \frac{1}{1}\;\rightarrow\;\boxed{a\neq-\frac{1}{2}}[/latex]
Aplicando a sua decoreba nas equações 2 e 3:
[latex]\left\{\begin{matrix} (10.3^{a}-3)x+y=1\\ x+y=0 \end{matrix}\right.\;\rightarrow\;\frac{(10.3^{a}-3)}{1}\neq \frac{1}{1}\;\rightarrow\;\boxed{a\neq \log_3{(\frac{2}{5})}}[/latex]
Perceba, por fim, que a sua decoreba nos dá relações válidas, que seriam suficientes se tivéssemos apenas 2 equações. Porém, como temos 3 equações, ela se tornam relações necessárias, mas não suficientes.
Como exemplo, a=0 é um caso particular que satisfaz as relações encontradas anteriormente, mas que não torna o sistema com as 3 equações SPD.
OBS: Como conselho geral, eu te diria para não usar esse tipo de decoreba, porque por mais que te dê alguma agilidade, há situações como esta, em que pode falhar. A melhor forma de resolver questões de sistemas é usar a receita de bolo que fiz na minha última resposta, pois dá sempre certo (note inclusive que cheguei nas mesmas relações que chegamos aplicando a sua decoreba).
Para fazer isso, a ideia é pensar que em um SPD com 2 incógnitas, é obrigatório ter 2 equações. Logo, duas equações do sistema da questão tem que ser necessariamente iguais. Evidentemente, a única forma disso ocorrer seria a equação 1 ser igual a 3 (fazendo essa igualdade, já encontraríamos os valores de a e resolveríamos a questão, mas vamos prosseguir na sua dúvida).
Feito isso, reduzimos o sistema para duas equações, que podem ser as equações 1 e 2 ou 2 e 3.
Aplicando a sua decoreba nas equações 1 e 2:
[latex]\left\{\begin{matrix} 3^{2a+1}x+y=1\\ x+y=0 \end{matrix}\right.\;\rightarrow\;\frac{3^{2a+1}}{1}\neq \frac{1}{1}\;\rightarrow\;\boxed{a\neq-\frac{1}{2}}[/latex]
Aplicando a sua decoreba nas equações 2 e 3:
[latex]\left\{\begin{matrix} (10.3^{a}-3)x+y=1\\ x+y=0 \end{matrix}\right.\;\rightarrow\;\frac{(10.3^{a}-3)}{1}\neq \frac{1}{1}\;\rightarrow\;\boxed{a\neq \log_3{(\frac{2}{5})}}[/latex]
Perceba, por fim, que a sua decoreba nos dá relações válidas, que seriam suficientes se tivéssemos apenas 2 equações. Porém, como temos 3 equações, ela se tornam relações necessárias, mas não suficientes.
Como exemplo, a=0 é um caso particular que satisfaz as relações encontradas anteriormente, mas que não torna o sistema com as 3 equações SPD.
OBS: Como conselho geral, eu te diria para não usar esse tipo de decoreba, porque por mais que te dê alguma agilidade, há situações como esta, em que pode falhar. A melhor forma de resolver questões de sistemas é usar a receita de bolo que fiz na minha última resposta, pois dá sempre certo (note inclusive que cheguei nas mesmas relações que chegamos aplicando a sua decoreba).

Victor011- Fera

- Mensagens : 663
Data de inscrição : 21/10/2015
Idade : 26
Localização : Rio de Janeiro, Brasil
Jvictors021 gosta desta mensagem
 Re: Discussão de sistemas
Re: Discussão de sistemas
Olá meu caro, intendi perfeitamente seu raciocínio, não sabia dessas questões abordadas, peguei um sistema simples para resolver e consegui resolver usando sua ideia... vou tentar representa-lo abaixoVictor011 escreveu:Essa decoreba que você está tentando usar é para sistemas com 2 incógnitas e 2 equações, enquanto que na questão temos 2 incógnitas e 3 equações. A única forma de conseguir usar essa decoreba seria reduzindo o número de equações da questão.
Para fazer isso, a ideia é pensar que em um SPD com 2 incógnitas, é obrigatório ter 2 equações. Logo, duas equações do sistema da questão tem que ser necessariamente iguais. Evidentemente, a única forma disso ocorrer seria a equação 1 ser igual a 3 (fazendo essa igualdade, já encontraríamos os valores de a e resolveríamos a questão, mas vamos prosseguir na sua dúvida).
Feito isso, reduzimos o sistema para duas equações, que podem ser as equações 1 e 2 ou 2 e 3.
Aplicando a sua decoreba nas equações 1 e 2:
[latex]\left\{\begin{matrix} 3^{2a+1}x+y=1\\ x+y=0 \end{matrix}\right.\;\rightarrow\;\frac{3^{2a+1}}{1}\neq \frac{1}{1}\;\rightarrow\;\boxed{a\neq-\frac{1}{2}}[/latex]
Aplicando a sua decoreba nas equações 2 e 3:
[latex]\left\{\begin{matrix} (10.3^{a}-3)x+y=1\\ x+y=0 \end{matrix}\right.\;\rightarrow\;\frac{(10.3^{a}-3)}{1}\neq \frac{1}{1}\;\rightarrow\;\boxed{a\neq \log_3{(\frac{2}{5})}}[/latex]
Perceba, por fim, que a sua decoreba nos dá relações válidas, que seriam suficientes se tivéssemos apenas 2 equações. Porém, como temos 3 equações, ela se tornam relações necessárias, mas não suficientes.
Como exemplo, a=0 é um caso particular que satisfaz as relações encontradas anteriormente, mas que não torna o sistema com as 3 equações SPD.
OBS: Como conselho geral, eu te diria para não usar esse tipo de decoreba, porque por mais que te dê alguma agilidade, há situações como esta, em que pode falhar. A melhor forma de resolver questões de sistemas é usar a receita de bolo que fiz na minha última resposta, pois dá sempre certo (note inclusive que cheguei nas mesmas relações que chegamos aplicando a sua decoreba).
3x +ky =2
-x +y =-1
x = (2-ky)/3
x = y + 1
(2-ky)/3 = y + 1 --> y(3+k) = 1 ---> k diferente de -3
Estou aprendendo a mexer no fórum por isso Não usei LATEX, mas muito obrigado pelo comprometimento em me ajudar!!

Jvictors021- Estrela Dourada

- Mensagens : 1116
Data de inscrição : 02/07/2021
Idade : 21
Localização : Passa Quatro - MG
Victor011 gosta desta mensagem
 Re: Discussão de sistemas
Re: Discussão de sistemas
Boa, essa é a ideia mesmo! Fico feliz em ajudar 
Quanto ao LATEX, não se preocupe hehe realmente ele é meio complicado/trabalhoso, mas continue praticando que com o tempo fica mais natural

Quanto ao LATEX, não se preocupe hehe realmente ele é meio complicado/trabalhoso, mas continue praticando que com o tempo fica mais natural

Victor011- Fera

- Mensagens : 663
Data de inscrição : 21/10/2015
Idade : 26
Localização : Rio de Janeiro, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Discussão de Sistemas
» discussão de sistemas
» Discussão de sistemas lineares.
» Discussão de sistemas lineares
» Discussão De Sistemas Lineares
» discussão de sistemas
» Discussão de sistemas lineares.
» Discussão de sistemas lineares
» Discussão De Sistemas Lineares
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












