Equações e inequações trigonométricas
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
 Equações e inequações trigonométricas
Equações e inequações trigonométricas
Última edição por DGL72021 em Sáb 17 Jul 2021, 02:13, editado 3 vez(es)
DGL72021- Jedi

- Mensagens : 209
Data de inscrição : 11/02/2021
 R: EQUAÇÕES E INEQUAÇÕES TRIGONOMÉTRICAS
R: EQUAÇÕES E INEQUAÇÕES TRIGONOMÉTRICAS
E aí DGL72021, tudo bem?
Podemos resolver da seguinte forma:
[latex]\left \{ \begin{array}{l} \sin 2x_{1}=\frac{\sqrt{3}}{2}\;\Rightarrow\;2x_{1}=\frac{\pi}{3}\;\therefore\;\boxed{x_{1}=\frac{\pi}{6}} \\\\ \sin 2x_{2}=\frac{\sqrt{3}}{2}\;\Rightarrow\;2x_{2}=\frac{2\pi}{3}\;\therefore\;\boxed{x_{2}=\frac{2\pi}{6}=\frac{\pi}{3}} \end{array} \right.[/latex]
Note que ambos os ângulos estão dentro do intervalo delimitado no enunciado, então, vamos adicionar π neles para encontrarmos seus semelhantes, dessa forma:
[latex]\left \{ \begin{array}{l} x_{3}=\frac{\pi}{6}+\pi\;\therefore\;\boxed{x_{3}=\frac{7\pi}{6}} \\\\ x_{4}=\frac{\pi}{3}+\pi\;\therefore\;\boxed{x_{4}=\frac{4\pi}{3}} \end{array} \right.[/latex]
Repare agora que caso continuássemos adicionando pi aos valores conseguintes obteríamos resultados fora do intervalo solicitado, ou seja, nosso conjunto solução será S={π/3; π/6; 7π/6; 4π/3}
Espero ter ajudado
Podemos resolver da seguinte forma:
[latex]\left \{ \begin{array}{l} \sin 2x_{1}=\frac{\sqrt{3}}{2}\;\Rightarrow\;2x_{1}=\frac{\pi}{3}\;\therefore\;\boxed{x_{1}=\frac{\pi}{6}} \\\\ \sin 2x_{2}=\frac{\sqrt{3}}{2}\;\Rightarrow\;2x_{2}=\frac{2\pi}{3}\;\therefore\;\boxed{x_{2}=\frac{2\pi}{6}=\frac{\pi}{3}} \end{array} \right.[/latex]
Note que ambos os ângulos estão dentro do intervalo delimitado no enunciado, então, vamos adicionar π neles para encontrarmos seus semelhantes, dessa forma:
[latex]\left \{ \begin{array}{l} x_{3}=\frac{\pi}{6}+\pi\;\therefore\;\boxed{x_{3}=\frac{7\pi}{6}} \\\\ x_{4}=\frac{\pi}{3}+\pi\;\therefore\;\boxed{x_{4}=\frac{4\pi}{3}} \end{array} \right.[/latex]
Repare agora que caso continuássemos adicionando pi aos valores conseguintes obteríamos resultados fora do intervalo solicitado, ou seja, nosso conjunto solução será S={π/3; π/6; 7π/6; 4π/3}
Espero ter ajudado
Última edição por gabriel de castro em Ter 13 Jul 2021, 21:34, editado 1 vez(es) (Motivo da edição : Correções textuais)
____________________________________________
"Alguns dos nossos desejos só se cumprem no outro, os pesadelos pertencem a nós mesmos" - Milton Hatoum

gabriel de castro- Elite Jedi

- Mensagens : 481
Data de inscrição : 01/05/2021
Idade : 21
Localização : Manaus, AM
Rory Gilmore e DGL72021 gostam desta mensagem
 Re: Equações e inequações trigonométricas
Re: Equações e inequações trigonométricas
O semelhante de ∏ /6 não seria 5∏/6? 7∏/6 = -1/2 e 5∏/6=1/2? 7∏/6 não estaria no terceiro quadrante e seria negativo?
x+∏/6= ∏
x= ∏- ∏/6
x=5∏/6
Agradeço desde já a ajuda, só tirar essa dúvida.
x+∏/6= ∏
x= ∏- ∏/6
x=5∏/6
Agradeço desde já a ajuda, só tirar essa dúvida.
DGL72021- Jedi

- Mensagens : 209
Data de inscrição : 11/02/2021
 Re: Equações e inequações trigonométricas
Re: Equações e inequações trigonométricas
Concordo contigo que π/6 e 5π/6 são semelhantes, mas ponha eles na equação dada (sen2x) e verá que eles resultarão em números opostos; reitero que quando adicionamos o π garantimos que isso não irá acontecer, estaremos mantendo as propriedades. Enfim, acredito que esteja esquecendo desse fator 2 e/ou talvez tenha me expressado mal, mas os semelhantes se referem ao resultados que obteremos ao efetuarmos o cálculo por meio da função. Aliás, esse é o gráfico dela:
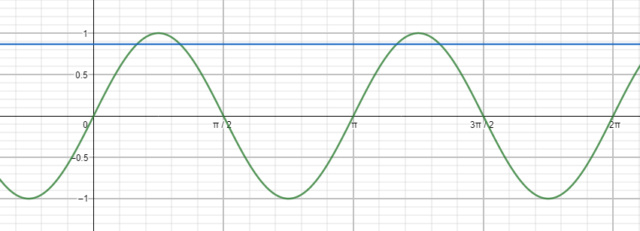
Obs.: A linha azul representa o √3/2.
Qualquer dúvida remanescente estou a seu dispor

Obs.: A linha azul representa o √3/2.
Qualquer dúvida remanescente estou a seu dispor
____________________________________________
"Alguns dos nossos desejos só se cumprem no outro, os pesadelos pertencem a nós mesmos" - Milton Hatoum

gabriel de castro- Elite Jedi

- Mensagens : 481
Data de inscrição : 01/05/2021
Idade : 21
Localização : Manaus, AM
Rory Gilmore e DGL72021 gostam desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» Equações e inequações trigonométricas
» Equações e inequações trigonométricas
» Equações e inequações trigonométricas
» Equações e inequações trigonométricas
» Equações e inequações trigonométricas
» Equações e inequações trigonométricas
» Equações e inequações trigonométricas
» Equações e inequações trigonométricas
» Equações e inequações trigonométricas
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













