Ponto de encontro MMC

Sobre uma pista circular de ciclismo existem 6 pontos de observação igualmente espaçados, indicados com as letras A, B, C, D, E e F. Dada a largada de uma corrida, dois ciclistas partem do ponto A e percorrem a pista no sentido da seta, como indicado na figura abaixo. Um deles completa uma volta a cada 5 minutos, e o outro, mais lento, completa uma volta a cada 8 minutos. As velocidades dos ciclistas são constantes.

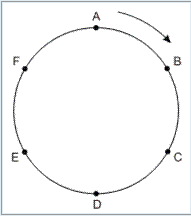
Considerando essas informações,
a) DETERMINE em qual dos pontos de observação os dois ciclistas irão se encontrar pela primeira vez depois da largada.

b) Um cronômetro zerado é ligado no momento da largada e é desligado assim que os dois ciclistas se encontram pela segunda vez. DETERMINE os minutos e segundos mostrados pelo cronômetro neste instante.


Eu estava tentando fazer por velocidade relativa, mas não estou conseguindo concluir.Gostaria de ver resolução tanto da forma física(vel relativa) quanto por métodos puramente matemáticos.

Para facilitar as contas, vamos supor que a pista tenha 1 200 m de perímetro.

Distância ente cada dois dos seis pontos = 1200/6 = 200 m

Va = 1 200/5 ---> Va = 240 m/min
Vb = 1 200/8 ---> Vb = 150 m/min

Quando A dá a 1ª volta completa (em 5 min) B anda: d'B = 5.150 = 750 m

Quando A dá a 2ª volta completa (em 5 min) B anda: d"B = 750 m --> 

B está a 750 + 750 - 1200 = 300 m à frente de A (entre B e C)

Seja x a distância percorrida por B, num tempo t, até o encontro ---> x = 150.t ---> I

Neste mesmo tempo A andou ---> 300 + x = 240.t  ---> II

I em II ---> 300 + 150.t = 240.t ---> t = 10/3 min

I --> x = 150.10/3 ---> x = 500 m

300 + 500 = 800 m ---> 800/200 = 4 ---> A, B, C, D, E

Muito obrigado @Elcioschin , consegui compreender .