Algebra Linear
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Algebra Linear
por Omagodasexatas3,14 Sex 19 Mar 2021, 12:55
Sejam: V,U espaços vetoriais sobre os reais, subespaços S,R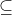 
V, com S 
R = 0 e transformações lineares L: R→U e M: S→U. Mostre que a transformação T: R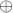
S → U definida via T(x+y) = L(x) + M(y) para x ∈ R, y ∈ S, é linear.
Omagodasexatas3,14- Recebeu o sabre de luz
- Mensagens : 111
Data de inscrição : 07/09/2017
Idade : 28
Localização : São Paulo, São paulo, Brasil
Tópicos semelhantes» Seja T é uma aplicação linear de um espaço vetorial (Algebra Linear)
» algebra linear:Ache uma aplicação linear
» 5.Ache uma aplicação linear T : R^4 --> R^3 (Algebra linear)
» ALGEBRA LINEAR - DEPENDENCIA LINEAR
» Combinação Linear LI ou LD (Álgebra Linear)
» algebra linear:Ache uma aplicação linear
» 5.Ache uma aplicação linear T : R^4 --> R^3 (Algebra linear)
» ALGEBRA LINEAR - DEPENDENCIA LINEAR
» Combinação Linear LI ou LD (Álgebra Linear)
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
