Problemas

Uma pessoa passou a sentir desconforto  após alimentar-se de forma inadequada numa festa entre amigos. Vendo que a situação não dava sinais de melhoras, foi consultar seu médico. Após alguns exames, o médico avaliou que a situação do paciente requeria tratamentos a base de dois medicamentos A e B. Esse tratamento deveria durar 30 dias segundo o planejamento descrito conforme abaixo:
 
• Ingestão do medicamento A durante alguns dias;
• Ingestão do medicamento B durante outros dias;
• Ingestão dos dois medicamentos em mais alguns dias;
• Por fim, não utilizar nenhum dos dois medicamentos em outros dias.
 
No retorno ao consultório do seu médico, o paciente relatou como procedeu na aplicação das recomendações médicas:
 
• Os medicamentos A e B foram ingeridos, juntos, em uma quantidade de dias igual à quantidade em que não ingeriu nenhum deles.
• O medicamento B foi ingerido em uma quantidade de dias igual ao dobro do número de dias da ingestão do medicamento A.
 
O paciente ingeriu o medicamento B durante quantos dias?
 
1) 20
2) 18
3) 10
4) 8
5) 2
 
Obs: Infelizmente não tenho a resposta dessa questão. O gabarito ainda vai ser divulgado.

A sozinho durante x dias
B sozinho durante 2.x dias
A + B durante w dias
Nenhum durante w dias 

x + 2.x + w + w = 30 ---> 3.x + 2.w = 30 ---> x deve ser par

Soluções possíveis:

A ... B .... A+B .... N
2 ... 4 ...... 12 .... 12
4 ... 8 ....... 9 ...... 9
6 .. 12 ...... 6 ...... 6
8 .. 16 ...... 3 ...... 3

A grande questão é se esse número de dias que A e B foram ingeridos inclui quando foram ingeridos juntos. Mas pelo enunciado parece ser 8 dias mesmo.

Elcioschin escreveu:A sozinho durante x dias
B sozinho durante 2.x dias
A + B durante w dias
Nenhum durante w dias 

x + 2.x + w + w = 30 ---> 3.x + 2.w = 30 ---> x deve ser par

Soluções possíveis:

A ... B .... A+B .... N
2 ... 4 ...... 12 .... 12
4 ... 8 ....... 9 ...... 9
6 .. 12 ...... 6 ...... 6
8 .. 16 ...... 3 ...... 3

Olá Elcioschin e Nickds1. É uma questão de um simulado e o gabarito saiu ontem. A resposta, segundo o gabarito é 20, mas não entendi porque. Eu achei 18 numa resolução que fiz e vou colocar abaixo. Quanto à observação de Nick, também achei que a questão não foi clara ao se referir apenas a B ou sempre que B foi utilizado, mas considerei a união das possibilidades.

Minha resolução:

A --> x dias
B --> y dias
A e B --> z dias
nem B nem B --> w dias

z = w   e   y = 2x
x + y + z + w = 30  -->  x + 2x + z + z = 30  -->  3x + 2z = 30

Aí eu comecei a testar pelas alternativas:
Para y = 20 --> x = 10
Mas aí veio a duvida que Nick também teve, y + x já corresponde a 30 dias.
Para y = 18 --> x = 9
y + x = 27 dias. Não bate também.
Enfim....

Hoje, porém, após o gabarito, fiz de outra maneira. Vejam se estou certo:


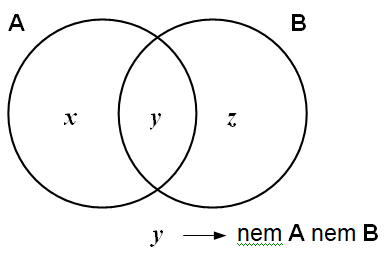
A: x + y
B: y + z
B é o dobro de A: y + z = 2(x + y)  -->  z = x + 2y

x + 2y + z = 30
x + 2y + x + 2y = 30
3x + 3y = 30
x + y = 10  --> quantidade de A
Portanto: B = 20
Foi meu segundo raciocínio após o gabarito.

Eu avisei que daria esse problema e deu. Sabe por quê? Porque, como eu disse, quando o enunciado fala em "ingeriu A em Y dias". Esse Y inclui quando ele ingeriu A e B juntos.

A solução é simples: a intersecção é A e B = k, não tomou = k

Logo, a união dos dois conjuntos é

A+2A-k+k = 30
3A = 30
A = 10

B = 2A = 20

Nickds12 escreveu:Eu avisei que daria esse problema e deu. Sabe por quê? Porque, como eu disse, quando o enunciado fala em "ingeriu A em Y dias". Esse Y inclui quando ele ingeriu A e B juntos.

A solução é simples: a intersecção é A e B = k, não tomou = k

Logo, a união dos dois conjuntos é

A+2A-k+k = 30
3A = 30
A = 10

B = 2A = 20

Mas aí você me deixou com uma dúvida. Os k dias em que ele não tomou nenhum medicamento estãp fora dos 30 dias? Pra mim eles estão dentro desse prazo, por isso considerei na soma.

Ao considerar B=20, ele não deixou de tomar o medicamento nenhum dia.