IME - NUMEROS COMPLEXOS
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
IME - NUMEROS COMPLEXOS
por Chance Única Seg 15 Mar 2021, 16:06
(IME 2020) Seja ???? = { ???? ∈ ???? | 2 ≤ |???? − 3 − 4????| ≤ 3} onde ???? é o conjunto dos números complexos. O valor do produto entre o simétrico do complexo de menor módulo do conjunto ???? e o conjugado do complexo de maior módulo do mesmo conjunto ???? é:
(A) -16 (B) -8 (C) -16/5 (D) 1 (E) 16
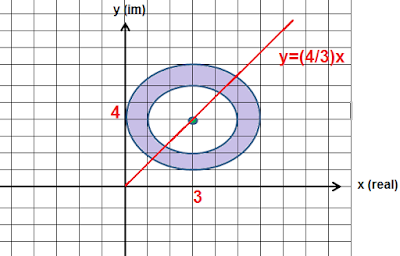
Ao determinar o módulo na resolução foi traçado uma reta que parte da origem do plano de Argand-Gauss e passa pelo ponto (3,4) que é o centro das circunferências concêntricas, alguém poderia me explicar o motivo do menor e maior módulo necessariamente estarem contidos nessa reta?
Chance Única- Iniciante
- Mensagens : 8
Data de inscrição : 09/03/2021
Re: IME - NUMEROS COMPLEXOS
por Chance Única Seg 15 Mar 2021, 16:10
Ví que o enunciado saiu com erros, reenviarei aqui (não deu erro na pré-visualização)...
Seja A = {z ∈ C | 2 ≤ |z - 3 - 4i| ≤ 3} onde C é o conjunto dos números complexos. O valor do produto entre o simétrico do complexo de menor módulo do conjunto A e o conjugado do complexo de maior módulo do mesmo conjunto A é:
Seja A = {z ∈ C | 2 ≤ |z - 3 - 4i| ≤ 3} onde C é o conjunto dos números complexos. O valor do produto entre o simétrico do complexo de menor módulo do conjunto A e o conjugado do complexo de maior módulo do mesmo conjunto A é:
Chance Única- Iniciante
- Mensagens : 8
Data de inscrição : 09/03/2021
Re: IME - NUMEROS COMPLEXOS
por Nickds12 Seg 15 Mar 2021, 17:33
Eu pensei em equações modulares.
z-3-4i = -2
z = 4i+1 -- simétrico = -4i-1
z-3-4i = -3
z = 4i ---- conjugado = -4i
(-4i)(-4i-1) --- -16+4i
z-3-4i = -2
z = 4i+1 -- simétrico = -4i-1
z-3-4i = -3
z = 4i ---- conjugado = -4i
(-4i)(-4i-1) --- -16+4i
Nickds12- Mestre Jedi
- Mensagens : 577
Data de inscrição : 31/08/2019
Idade : 27
Localização : RJ
Tópicos semelhantes» números complexos FME
» Números Complexos
» Numeros Complexos
» ITA - Números complexos
» Números Complexos
» Números Complexos
» Numeros Complexos
» ITA - Números complexos
» Números Complexos
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
