(Unicentro)
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
(Unicentro)
por Paracelso_Zn Seg 01 Fev 2021, 20:40
02- Seja f(x) = x² , f :ℜ → ℜ . Sejam as famílias de funções do tipo: g(x) = k.f(x), h(x) = f(x) + k e t(x) = f(x + k) ,
onde k é uma constante real e diferente de zero. Sobre essas famílias, considere as afirmativas a seguir.
I. As curvas da família g se interceptam em apenas um ponto.
II. As curvas da família h não se interceptam.
III. Cada par de curvas da família t se intercepta em dois pontos.
IV. Existem curvas da família g e t que não se interceptam.
Estão corretas apenas as afirmativas:
a) I e II.
b) I e III.
c) III e IV.
d) I, II e IV.
e) II, III e IV.
Nunca vi exercício parecido, estou muito perdido, as "curvas" que ele diz se refere aos gráficos das funções?
onde k é uma constante real e diferente de zero. Sobre essas famílias, considere as afirmativas a seguir.
I. As curvas da família g se interceptam em apenas um ponto.
II. As curvas da família h não se interceptam.
III. Cada par de curvas da família t se intercepta em dois pontos.
IV. Existem curvas da família g e t que não se interceptam.
Estão corretas apenas as afirmativas:
a) I e II.
b) I e III.
c) III e IV.
d) I, II e IV.
e) II, III e IV.
- gab:
- D
Nunca vi exercício parecido, estou muito perdido, as "curvas" que ele diz se refere aos gráficos das funções?
Última edição por Paracelso_Zn em Seg 01 Fev 2021, 21:38, editado 1 vez(es)
Paracelso_Zn- Padawan
- Mensagens : 69
Data de inscrição : 29/01/2021
Idade : 28
Localização : Paraná
Re: (Unicentro)
por Emanuel Dias Seg 01 Fev 2021, 20:47
Olá.
Isso, cada esboço de gráfico é chamado de curva.
Família de curva é todas as possibilidades de gráfico que podem surgir de uma função.
Vou dar uma ideia você prossegue, pode ser?
Veja:
f(x)=x² é a parábola que passa na origem.
g(x)=kf(x) é uma parábola geral, veja que f(x) é um caso específico dessa, onde k=1.
Veja o comportamento da parábola se k varia, ao fundo deixei esboçado f(x).
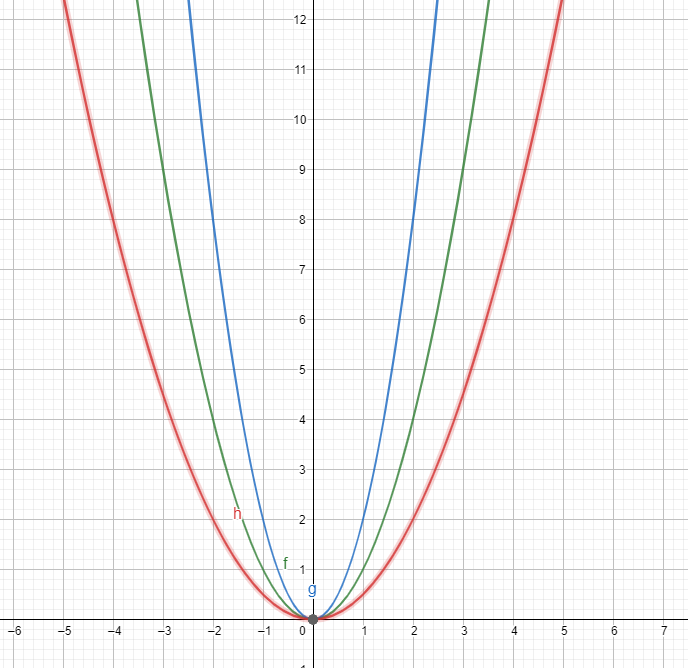
Cada um dos esboços é uma curva da família g, note que só se encontram em um único ponto.
verde=x²
vermelho=x²/2
azul=2x²
Se continuar esboçando para k qualquer vai fechar o gráfico mas elas se tocam em apenas um ponto, sempre em x=y=0
Tenta para as outras.
Isso, cada esboço de gráfico é chamado de curva.
Família de curva é todas as possibilidades de gráfico que podem surgir de uma função.
Vou dar uma ideia você prossegue, pode ser?
Veja:
f(x)=x² é a parábola que passa na origem.
g(x)=kf(x) é uma parábola geral, veja que f(x) é um caso específico dessa, onde k=1.
Veja o comportamento da parábola se k varia, ao fundo deixei esboçado f(x).
Cada um dos esboços é uma curva da família g, note que só se encontram em um único ponto.
verde=x²
vermelho=x²/2
azul=2x²
Se continuar esboçando para k qualquer vai fechar o gráfico mas elas se tocam em apenas um ponto, sempre em x=y=0
Tenta para as outras.
____________________________________________
El Álgebra no es más que Geometría y la Geometría no es más que Álgebra abstracta
Sophie Germain
Sophie Germain
Emanuel Dias- Monitor
- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
Paracelso_Zn gosta desta mensagem
Re: (Unicentro)
por Paracelso_Zn Seg 01 Fev 2021, 21:38
Consegui entender a ideia de "curvas da família", obrigado Emanuel!
Paracelso_Zn- Padawan
- Mensagens : 69
Data de inscrição : 29/01/2021
Idade : 28
Localização : Paraná
Emanuel Dias gosta desta mensagem
Tópicos semelhantesPiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
