Arcos

por joice21 Qui 09 Jul 2020, 12:32

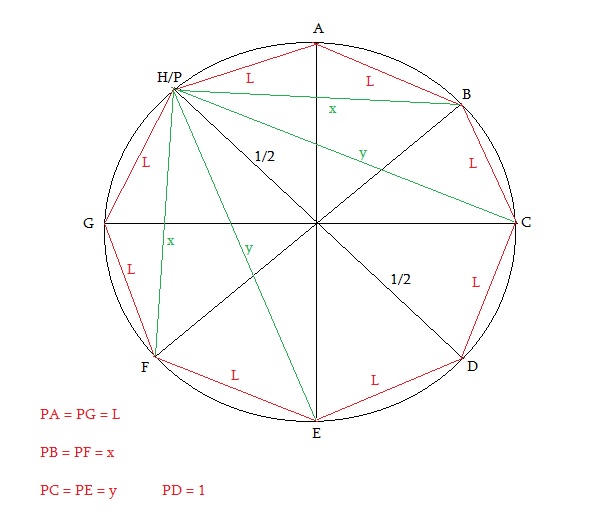
Na figura, ABCDEFGH é um octógono regular inscrito em
uma circunferência de diámetro com medida 1.
Sendo P um ponto do menor arco AH desta circunferência, a soma
PA^2 + PB^2+ PC^2 + PD^2 + PE^2 + PF^2 + PG^2 + PH^2 é
igual a
a) 4
b) 5
c) 6
d) 8
e)9/2
Link da foto.
https://pt-static.z-dn.net/files/d03/1380c8c9b73eb34229256a2dc59a91e5.jpg

se puderem colocar o passo a passo eu agradeço!

por **Elcioschin** Qui 09 Jul 2020, 13:14

Para facilitar, como o ponto P está em qualquer ponto do arco AH vou fazer P = H:

CD² = OC² + OD² - 2.OC.OD.cos(CÔD) ---> L² = r² + r² - 2.r².cos45º --->

L² = (1/2)² + (1/2)² - 2.(1/2)².(√2/2) ---> L² = (2 - √2)/4

PB² = AP² + AB² - 2.AP.AB.cos(PAB) ---> x² = L² + L² - 2.L².cos(135º) --->

x² = L²(2 + √2)

No trapézio ABCP: PC = AP.cos(A^PC) + BC.cosB^CP) + AB --->

y = L.√2/2) + L + L.√2/2) ---> y = L.(√2 + 1) ---> y² = L².(3 + 2.√2)

Complete

por joice21 Qui 09 Jul 2020, 15:36

Elcioschin escreveu:Para facilitar, como o ponto P está em qualquer ponto do arco AH vou fazer P = H:

CD² = OC² + OD² - 2.OC.OD.cos(CÔD) ---> L² = r² + r² - 2.r².cos45º --->

L² = (1/2)² + (1/2)² - 2.(1/2)².(√2/2) ---> L² = (2 - √2)/4

PB² = AP² + AB² - 2.AP.AB.cos(PAB) ---> x² = L² + L² - 2.L².cos(135º) --->

x² = L²(2 + √2)

No trapézio ABCP: PC = AP.cos(A^PC) + BC.cosB^CP) + AB --->

y = L.√2/2) + L + L.√2/2) ---> y = L.(√2 + 1) ---> y² = L².(3 + √2)

Complete

Como que [latex]\sqrt{2}+ 1 fica \sqrt{2}+3[/latex]

por **Vitor Ahcor** Qui 09 Jul 2020, 15:47

Uma outra ideia:

Ao ligarmos dois vértices diametralmente opostos a P, teremos um triângulo retângulo de hipotenusa igual ao diâmetro da circunferência. Desenhei somente dois triângulos, mas no total serão 4. O que a questão nos pede é a soma dos quadrados dos catetos desses quatro triângulos, ou seja, quatro vezes o diâmetro ao quadrado. Desse modo a resposta é 4*1² = 4.