Atrito no plano inclinado
2 participantes
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
Atrito no plano inclinado
por Carolina1502 Qua 01 Jul 2020, 15:11
A figura a seguir mostra dois recipientes de massas desprezíveis e interligados. Com o recipiente A contendo 4 kg de água e o recipiente B vazio, o conjunto permanece em repouso sobre o plano inclinado. Abrindo-se o registro, permite-se que parte da água passe, lentamente, para o recipiente B até que o conjunto fique na iminência de deslizar. Nessa situação, determine a massa de água no vaso A. Dados: sen de alfa = 0,6. Coeficientes de atrito estático entre os recipientes e o plano: A= 0,80 e B= 0,50.
Resolução:
- Spoiler:
- 10/3 kg
Carolina1502- Recebeu o sabre de luz
- Mensagens : 142
Data de inscrição : 08/09/2016
Idade : 27
Localização : Minas Gerais
Re: Atrito no plano inclinado
por Lucius Draco Qua 01 Jul 2020, 17:12
i) Na eminencia de movimento temos:
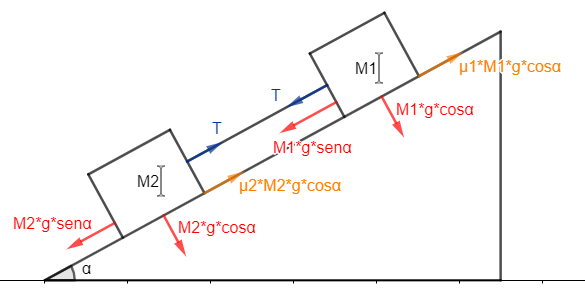
Com isso temos as relações:
[latex]\left\{\begin{matrix} M_{2}\cdot g\cdot \sin \alpha =T+\mu _{2}\cdot M_{2}\cdot g\cdot \cos \alpha \\ T+M_{1}\cdot g\cdot \sin \alpha =\mu _{1}\cdot M_{1}\cdot g\cdot \cos \alpha \end{matrix}\right.[/latex]
Logo,
[latex]M_{2}\cdot g\cdot \sin \alpha + M_{1}\cdot g\cdot \sin \alpha = \mu _{2}\cdot M_{2}\cdot g\cdot \cos \alpha + \mu _{1}\cdot M_{1}\cdot g\cdot \cos \alpha[/latex]
[latex](\mu _{1}\cdot \cos \alpha - \sin \alpha)\cdot M_{1} + (\mu _{2}\cdot \cos \alpha - \sin \alpha)\cdot M_{2}=0[/latex]
[latex](0.8\cdot 0.8 - 0.6)\cdot M_{1} + (0.5\cdot 0.8 - 0.6)\cdot M_{2}=0\Rightarrow 0.04\cdot M_{1} - 0.2\cdot M_{2}=0[/latex]
[latex]0.04\cdot M_{1} - 0.2\cdot M_{2}=0\Rightarrow M_{1}=5\cdot M_{2}[/latex]
Pelo enunciado temos que M1 + M2 = 4, logo:
[latex]M_{1}=5\cdot M_{2}\Rightarrow M_{1}=5\cdot (4-M_{1})\Rightarrow 6\cdot M_{1}=20\Rightarrow M_{1}=\frac{10}{3}kg[/latex]
Com isso temos as relações:
[latex]\left\{\begin{matrix} M_{2}\cdot g\cdot \sin \alpha =T+\mu _{2}\cdot M_{2}\cdot g\cdot \cos \alpha \\ T+M_{1}\cdot g\cdot \sin \alpha =\mu _{1}\cdot M_{1}\cdot g\cdot \cos \alpha \end{matrix}\right.[/latex]
Logo,
[latex]M_{2}\cdot g\cdot \sin \alpha + M_{1}\cdot g\cdot \sin \alpha = \mu _{2}\cdot M_{2}\cdot g\cdot \cos \alpha + \mu _{1}\cdot M_{1}\cdot g\cdot \cos \alpha[/latex]
[latex](\mu _{1}\cdot \cos \alpha - \sin \alpha)\cdot M_{1} + (\mu _{2}\cdot \cos \alpha - \sin \alpha)\cdot M_{2}=0[/latex]
[latex](0.8\cdot 0.8 - 0.6)\cdot M_{1} + (0.5\cdot 0.8 - 0.6)\cdot M_{2}=0\Rightarrow 0.04\cdot M_{1} - 0.2\cdot M_{2}=0[/latex]
[latex]0.04\cdot M_{1} - 0.2\cdot M_{2}=0\Rightarrow M_{1}=5\cdot M_{2}[/latex]
Pelo enunciado temos que M1 + M2 = 4, logo:
[latex]M_{1}=5\cdot M_{2}\Rightarrow M_{1}=5\cdot (4-M_{1})\Rightarrow 6\cdot M_{1}=20\Rightarrow M_{1}=\frac{10}{3}kg[/latex]
Lucius Draco- Jedi
- Mensagens : 234
Data de inscrição : 29/05/2020
Idade : 25
Localização : Fortaleza, CE
Tópicos semelhantes» Plano sem atrito
» Plano Inclinado - Atrito
» plano inclinado com atrito
» plano inclinado com atrito
» Atrito e plano inclinado
» Plano Inclinado - Atrito
» plano inclinado com atrito
» plano inclinado com atrito
» Atrito e plano inclinado
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
