Angulos de um triangulo
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Angulos de um triangulo
por Luciano Augusto Sex 05 Jun 2020, 10:46
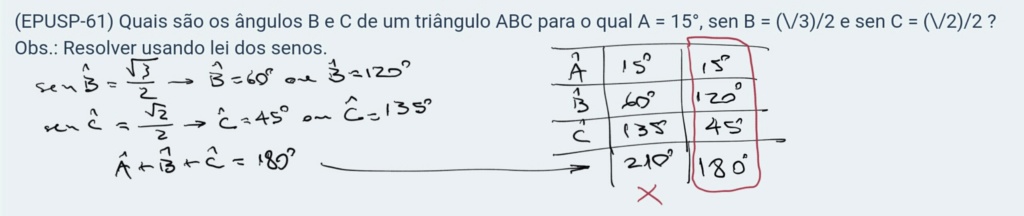
(EPUSP-61) Quais são os ângulos B e C de um triângulo ABC para o qual A = 15°, sen B = (\/3)/2 e sen C = (\/2)/2 ?
Obs.: Resolver usando lei dos senos.
Obs.: Resolver usando lei dos senos.
Luciano Augusto- Recebeu o sabre de luz
- Mensagens : 133
Data de inscrição : 21/07/2019
Idade : 23
Localização : Mogi das Cruzes - São Paulo - Brasil
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: Angulos de um triangulo
por Luciano Augusto Sex 05 Jun 2020, 11:27
Medeiros eu também de cara ja notei que era 60° e 45°, mas como a proposta era resolver ultilizando lei dos senos eu fiquei travado, teria alguma forma de resolver usando lei dos senos?
Luciano Augusto- Recebeu o sabre de luz
- Mensagens : 133
Data de inscrição : 21/07/2019
Idade : 23
Localização : Mogi das Cruzes - São Paulo - Brasil
Re: Angulos de um triangulo
por Medeiros Sex 05 Jun 2020, 11:45
A lei-dos-senos que eu conheço estabelece uma razão entre o lado e o seno do ângulo oposto a esse lado, e esta razão é constante para todos os lados de um mesmo triângulo.
Como o exercício não fornece lado algum, não vi como usar tal lei.
Talvez esteja-se querendo usar o seno da soma de arcos. Algo assim:
A + B + C = 180° -----> B + C = 180° - A
sen(B + C) = sen(180° - A) .......... ou ........... sen (A + B) = sen(180° - C)
e desenvolver ambos os membros até chegar numa conclusão.
Como o exercício não fornece lado algum, não vi como usar tal lei.
Talvez esteja-se querendo usar o seno da soma de arcos. Algo assim:
A + B + C = 180° -----> B + C = 180° - A
sen(B + C) = sen(180° - A) .......... ou ........... sen (A + B) = sen(180° - C)
e desenvolver ambos os membros até chegar numa conclusão.
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Tópicos semelhantes» Ângulos num triângulo
» Ângulos no Triângulo
» Ângulos no triângulo.
» Ângulos no triangulo
» Ângulos no triângulo
» Ângulos no Triângulo
» Ângulos no triângulo.
» Ângulos no triangulo
» Ângulos no triângulo
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
