(CN-87) - Teoria dos conjuntos

Considere os conjuntos A, B, C e U no diagrama abaixo. A região hachurada corresponde ao conjunto






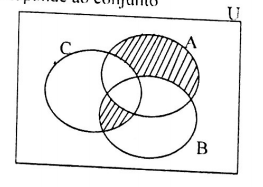
a) [A-(B\cap C)]\cup [(B\cap C)-A]

b) C_{[(A\cup B\cup C)]}^{[(A\cup B)-C]}

c) C_{A\cup (B\cap C)}^{[(A\cap B)\cup (A\cap C))])}

d) (A\cup B_)-[(A\cap B)\cup (A\cap C)]


Resposta:C

Como chega na resposta sem ser por tentativa?

Só consigo imaginar a resolução pondo uma letra minúscula em cada espaço e montando as equações por alternativa mesmo.

raquelvaladao escreveu:Só consigo imaginar a resolução pondo uma letra minúscula em cada espaço e montando as equações por alternativa mesmo.

Tem uma galera que consegue, só da figura, ir escrevendo onde x pertence e onde não pertence e chegar na resposta. Mas também só consigo testando alternativa por alternativa.

Esse tipo de questão se resolve olhando mesmo. Porque usando conjuntos temos

n(A U B U C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)

O que queremos é n(A)+ n(B ∩ C)

n(A U B U C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)
n(A) = n(A U B U C) - (+ n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)

n(A) + n(B ∩ C) = n(A U B U C) - (+ n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)) + n(B ∩ C)
n(A) + n(B ∩ C) = n(A U B U C) - n(B) - n(C) + n(A ∩ B) + n(A ∩ C) + n(B ∩ C) - n(A ∩ B ∩ C) + n(B ∩ C)

Vamos simplificar olhando o gráfico e estabelecendo equivalências

n(A) + n(B ∩ C) = n(A U B U C) - n(B) - n(C) + n(A ∩ B) + n(A ∩ C) + 2n(B ∩ C) - n(A ∩ B ∩ C) 

n(A U B U C) - n(B) - n(C)  = n(A) - n(A ∩ B) - n(A ∩ C) + n(A ∩ B ∩ C)

n(A) + n(B ∩ C) = n(A) - n(A ∩ B) - n(A ∩ C) + n(A ∩ B ∩ C) + n(A ∩ B) + n(A ∩ C) + 2n(B ∩ C) - n(A ∩ B ∩ C) 

n(A ∩ B) + n(A ∩ C) + n(B ∩ C) = n(A ∩ B ∩ C) + n(B ∩ C)

n(A) + n(B ∩ C) = n(A) - n(A ∩ B) - n(A ∩ C) + n(A ∩ B ∩ C)  + n(B ∩ C)  

Veja que equivale ao complementar do enunciado

n(AU(B ∩ C)) = n(A) -  n(A ∩ B) - n(A ∩ C) + n(B∩C)
n((A∩B)U(A∩C)) = n(A∩B) + n(A∩C) - n(A∩B∩C)

n(A) -  n(A ∩ B) - n(A ∩ C) + n(B∩C) - n(A∩B) - n(A∩C) + n(A∩B∩C)

Nickds12 escreveu:Esse tipo de questão se resolve olhando mesmo. Porque usando conjuntos temos

n(A U B U C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)

O que queremos é n(A)+ n(B ∩ C)

n(A U B U C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)
n(A) = n(A U B U C) - (+ n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)

n(A) + n(B ∩ C) = n(A U B U C) - (+ n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)) + n(B ∩ C)
n(A) + n(B ∩ C) = n(A U B U C) - n(B) - n(C) + n(A ∩ B) + n(A ∩ C) + n(B ∩ C) - n(A ∩ B ∩ C) + n(B ∩ C)

Vamos simplificar olhando o gráfico e estabelecendo equivalências

n(A) + n(B ∩ C) = n(A U B U C) - n(B) - n(C) + n(A ∩ B) + n(A ∩ C) + 2n(B ∩ C) - n(A ∩ B ∩ C) 

n(A U B U C) - n(B) - n(C)  = n(A) - n(A ∩ B) - n(A ∩ C) + n(A ∩ B ∩ C)

n(A) + n(B ∩ C) = n(A) - n(A ∩ B) - n(A ∩ C) + n(A ∩ B ∩ C) + n(A ∩ B) + n(A ∩ C) + 2n(B ∩ C) - n(A ∩ B ∩ C) 

n(A ∩ B) + n(A ∩ C) + n(B ∩ C) = n(A ∩ B ∩ C) + n(B ∩ C)

n(A) + n(B ∩ C) = n(A) - n(A ∩ B) - n(A ∩ C) + n(A ∩ B ∩ C)  + n(B ∩ C)  

Veja que equivale ao complementar do enunciado

n(AU(B ∩ C)) = n(A) -  n(A ∩ B) - n(A ∩ C) + n(B∩C)
n((A∩B)U(A∩C)) = n(A∩B) + n(A∩C) - n(A∩B∩C)

n(A) -  n(A ∩ B) - n(A ∩ C) + n(B∩C) - n(A∩B) - n(A∩C) + n(A∩B∩C)

Realmente, observando é bem mais prático, mas gosto de fazer de vários jeitos para aprender de diversas maneiras. Obrigado!

O melhor caminho pra esse tipo de questão é só usando algebra de conjuntos mesmo?