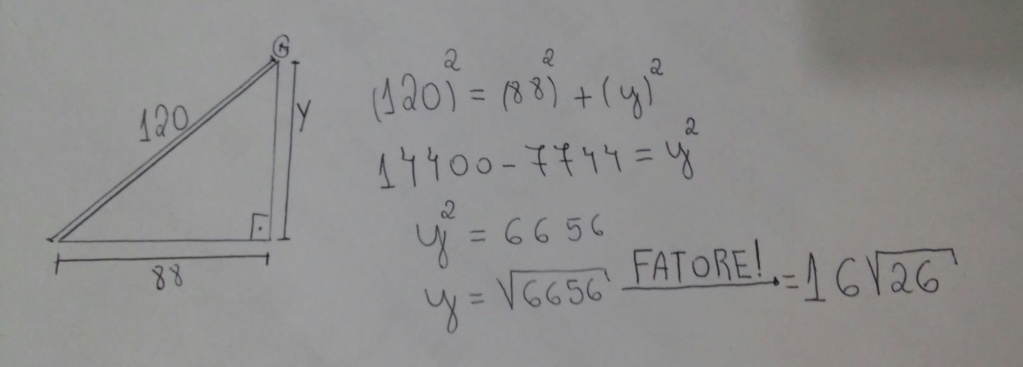Semelhança de triângulos - Geometria Plana
3 participantes
Página 1 de 1
 Semelhança de triângulos - Geometria Plana
Semelhança de triângulos - Geometria Plana
Os campos de petróleo Peroá (P) e Golfinho (G) distam, respectivamente, 56 km e 120 km de um ponto A do litoral, o qual estamos supondo retilíneo (veja a figura abaixo). Os pontos A e B são os pontos do litoral que estão mais próximos, respectivamente, dos campos P e G. A distância do ponto A ao ponto B é de 88 km. Deseja-se construir no litoral um pólo de gás que f ique situado à mesma distância dos campos P e G.

Gabarito: B
Obs: eu já encontrei essa mesma questão no site com a resposta mas não estou conseguindo interpretar. Se possível poderia adicionar a imagem da resolução usando semelhança de triângulos? Eu seria grata.

Gabarito: B
Obs: eu já encontrei essa mesma questão no site com a resposta mas não estou conseguindo interpretar. Se possível poderia adicionar a imagem da resolução usando semelhança de triângulos? Eu seria grata.
NMS50- Recebeu o sabre de luz

- Mensagens : 107
Data de inscrição : 04/03/2019
Idade : 24
Localização : Suzano, Sao Paulo, Brasil
 Re: Semelhança de triângulos - Geometria Plana
Re: Semelhança de triângulos - Geometria Plana
Quais as alternativas?

folettinhomed- Mestre Jedi

- Mensagens : 988
Data de inscrição : 23/02/2019
Idade : 24
Localização : Santa Cruz do Sul, RS, Brasil
 Re: Semelhança de triângulos - Geometria Plana
Re: Semelhança de triângulos - Geometria Plana
*Desculpa, as alternativas estão abaixo:
Nessas condições, pode-se afirmar que o pólo de gás deve ficar situado a:
a) 74 km de A e a 14 km de B.
b) 64 km de A e a 24 km de B.
c) 44 km de A e a 44 km de B.
d)24 km de A e a 64 km de B.
e)14 km de A e a 64 km de B.
Nessas condições, pode-se afirmar que o pólo de gás deve ficar situado a:
a) 74 km de A e a 14 km de B.
b) 64 km de A e a 24 km de B.
c) 44 km de A e a 44 km de B.
d)24 km de A e a 64 km de B.
e)14 km de A e a 64 km de B.
NMS50- Recebeu o sabre de luz

- Mensagens : 107
Data de inscrição : 04/03/2019
Idade : 24
Localização : Suzano, Sao Paulo, Brasil
 Re: Semelhança de triângulos - Geometria Plana
Re: Semelhança de triângulos - Geometria Plana
Acho que por analítica é beeeem mais fácil de resolver a questão. Segue o raciocínio:
Tomando o ponto A como origem de um plano cartesiano, podemos tratar as localizações como coordenadas:
A(0,0) ; B(88,0) ; P(0,56); G(88, 16√26)
*Não te assusta com o ponto G, depois posto uma imagem mostrando de onde surgiram esses números kkkk
Então, como o novo local deve ser equidistante dos pontos P e G, podemos usar a fórmula da distância entre dois pontos, chamando o novo local como (x,0) --> Perceba que a coordenada y é 0 pois o local deve ser no litoral, e adotei a linha do litoral como eixo x!!
Então: DPX : √(xP - xX)² + (yP - yX)²
√(x - 0)² + (56-0)²
DPX: √x² + 56²
Mantenhamos assim por enquanto.
DGX = √xG - xX)² + (yG - yX)²
√(x-88)² + (16√26 -0)²
√x² - 176x +7744 + 6656
√x² - 176x +14400
Agora que calculamos a distância de X a P e a distância de x a G, tu tens de perceber que essas distâncias tem que ser equivalentes, já que a questão quer que o novo local seja equidistante do ponto P e do G!!
Então:
[size=30] [/size]DPX = DGX
[size=30] [/size]√x² + 56² = √x² - 176x +14400
x² + 3136 = x² - 176x + 14400
-176x +11264 = 0
-176x = -11264
176x = 11264
x = 11264/176
x= 64
Dessa forma, o novo local, que tratamos por x, fica situado a 64 km de A e a (88-64) = 24 km de B
*Vou desenhar e depois posto!! Avisa se não entendeu!!
Tomando o ponto A como origem de um plano cartesiano, podemos tratar as localizações como coordenadas:
A(0,0) ; B(88,0) ; P(0,56); G(88, 16√26)
*Não te assusta com o ponto G, depois posto uma imagem mostrando de onde surgiram esses números kkkk
Então, como o novo local deve ser equidistante dos pontos P e G, podemos usar a fórmula da distância entre dois pontos, chamando o novo local como (x,0) --> Perceba que a coordenada y é 0 pois o local deve ser no litoral, e adotei a linha do litoral como eixo x!!
Então: DPX : √(xP - xX)² + (yP - yX)²
√(x - 0)² + (56-0)²
DPX: √x² + 56²
Mantenhamos assim por enquanto.
DGX = √xG - xX)² + (yG - yX)²
√(x-88)² + (16√26 -0)²
√x² - 176x +7744 + 6656
√x² - 176x +14400
Agora que calculamos a distância de X a P e a distância de x a G, tu tens de perceber que essas distâncias tem que ser equivalentes, já que a questão quer que o novo local seja equidistante do ponto P e do G!!
Então:
[size=30] [/size]DPX = DGX
[size=30] [/size]√x² + 56² = √x² - 176x +14400
x² + 3136 = x² - 176x + 14400
-176x +11264 = 0
-176x = -11264
176x = 11264
x = 11264/176
x= 64
Dessa forma, o novo local, que tratamos por x, fica situado a 64 km de A e a (88-64) = 24 km de B
*Vou desenhar e depois posto!! Avisa se não entendeu!!
Última edição por folettinhomed em Dom 08 Set 2019, 11:37, editado 3 vez(es)

folettinhomed- Mestre Jedi

- Mensagens : 988
Data de inscrição : 23/02/2019
Idade : 24
Localização : Santa Cruz do Sul, RS, Brasil

folettinhomed- Mestre Jedi

- Mensagens : 988
Data de inscrição : 23/02/2019
Idade : 24
Localização : Santa Cruz do Sul, RS, Brasil

folettinhomed- Mestre Jedi

- Mensagens : 988
Data de inscrição : 23/02/2019
Idade : 24
Localização : Santa Cruz do Sul, RS, Brasil
 Re: Semelhança de triângulos - Geometria Plana
Re: Semelhança de triângulos - Geometria Plana
Deu grande kkkkkkk

folettinhomed- Mestre Jedi

- Mensagens : 988
Data de inscrição : 23/02/2019
Idade : 24
Localização : Santa Cruz do Sul, RS, Brasil

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Re: Semelhança de triângulos - Geometria Plana
Re: Semelhança de triângulos - Geometria Plana
Muito obrigada Folettinhomed e Medeiros...eu consegui entender as duas resoluções. Agradeço muitíssimo!
NMS50- Recebeu o sabre de luz

- Mensagens : 107
Data de inscrição : 04/03/2019
Idade : 24
Localização : Suzano, Sao Paulo, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Geometria Plana - semelhança de triângulos.
» semelhança de triângulos geometria plana
» Geometria plana 2 (Semelhança)
» Geometria Plana - Triângulos
» semelhança geometria plana
» semelhança de triângulos geometria plana
» Geometria plana 2 (Semelhança)
» Geometria Plana - Triângulos
» semelhança geometria plana
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos