Achar a área da região limitada pelos gráficos

por @Khan@ Qua 26 Jun 2019, 23:58

Olá.

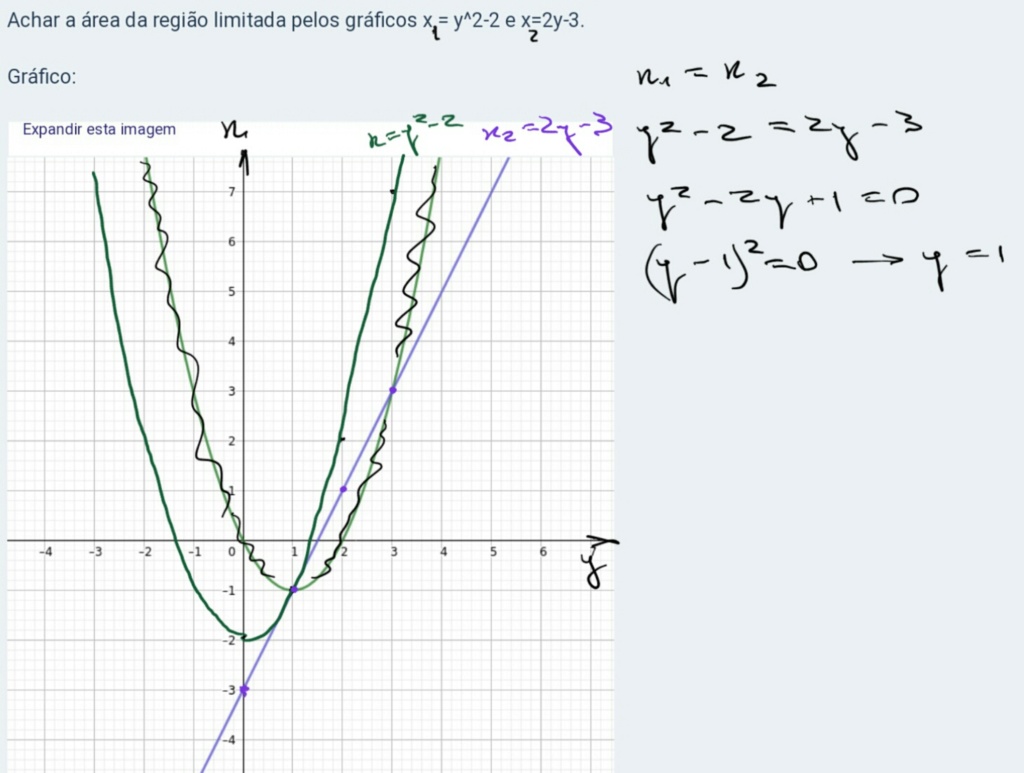
Achar a área da região limitada pelos gráficos x = y^2-2 e x=2y-3.

Gráfico:

Achar a área da região limitada pelos gráficos Selezz10

Minha dúvida é a seguinte: Como devo proceder com o cálculo?

Posso calcular a expressão de forma direta, com a seguinte fórmula:

\begin{aligned}\int ^{3}_{1}-y^{2}+4y-3 dy\end{aligned}

Ou de alguma forma teria de fazer outra conta para calcular a área que está no outro quadrante?

Meu resultado foi: \begin{aligned}\dfrac {2}{3}u.a.\\\end{aligned}

por **Medeiros** Qui 27 Jun 2019, 02:47

Não há área limitada pelas curvas dadas!

a reta é tangente à parábola no ponto (-1, 1).

Nota: os eixos estão trocados; o desenho da parábola está fora da posição.

Achar a área da região limitada pelos gráficos Scree410

por @Khan@ Qui 27 Jun 2019, 13:40

Realmente, percebi agora que os eixos estão trocados. Nos exercícios comumente fazíamos com y= x+c, passou despercebido esse pequeno detalhe.

Mas, voltando ao assunto, caso ocorresse algo assim, teria de calcular separado? Ou essa questão de calcular separado apenas faz-se quando "atravessa-se" o eixo y?

por @Khan@ Qui 27 Jun 2019, 16:04

Achar a área da região limitada pelos gráficos Czelcu11

Achar a área da região limitada pelos gráficos Selezz11

Cheguei nisso, mas meu gráfico não fecha.

A equação ficaria:
\begin{aligned}y^{2}-2y=2y-3\\ y^{2}-4y+3\\ \int ^{0}_{-1}-y^{2}+4y-3dy\cdot \end{aligned}

+

\begin{aligned}\int ^{3}_{0}y^{2}-4y+3dy\\\end{aligned}

*Não sei se devo aplicar os valor em y para a integral ou os valores em x, apliquei os em x.

por @Khan@ Qui 04 Jul 2019, 19:23

\begin{aligned}\int ^{3}_{1}-y^{2}+4y-3dy\\
\end{aligned}

Resposta: 4/3 u.a.

por **Elcioschin** Qui 04 Jul 2019, 20:14

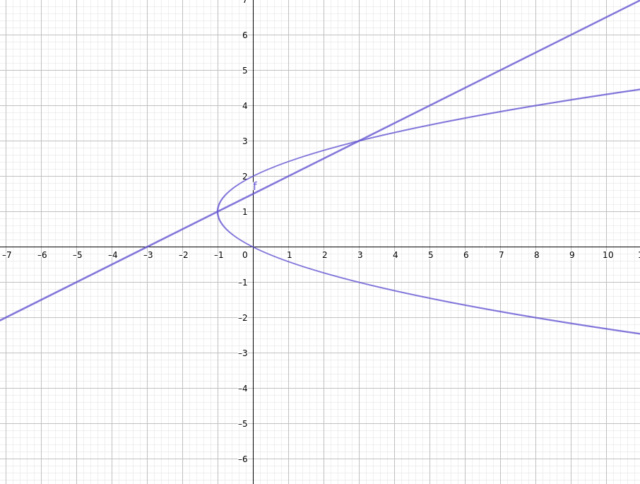
Seu novo gráfico está errado

x = y² - 2 ---> Para x = 0 ---> y = - √2 e y = +√2 ---> (0, -√2) e (0 +√2)

Assim, você desenhou erradamente o gráfico da parábola passando por (0, 0) e (0, 2)

E neste caso, continua a reta não interceptando a parábola em 2 pontos.