Semelhança de triângulos
3 participantes
Página 1 de 1
Semelhança de triângulos
por Emanuel Dias Qua 26 Jun 2019, 22:36
Na figura abaixo, AD=1/4AB, DE//BC, EF//AB, FG//AC e GH//BC. Então, EH/AC vale:
A)1/2 Gabarito: A
B)1/3
C)1/4
D)2/3
E)3/4
Devido ao paralelismo há vários triângulos semelhantes. Eu só encontro 1/4 como resposta.
A)1/2 Gabarito: A
B)1/3
C)1/4
D)2/3
E)3/4
Devido ao paralelismo há vários triângulos semelhantes. Eu só encontro 1/4 como resposta.
Emanuel Dias- Monitor
- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
Re: Semelhança de triângulos
por Medeiros Qua 26 Jun 2019, 23:39
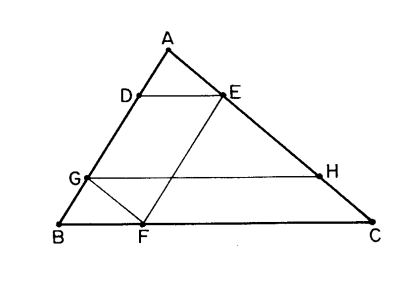
Triângulos ADE e GBF são congruentes. Então AD = GB = (1/4).AB, o que implica (pois é o que sobra) que DG = (1/2).AB.
Pelo teorema de Tales
DG/AB = EH/AC = 1/2
Pelo teorema de Tales
DG/AB = EH/AC = 1/2
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: Semelhança de triângulos
por Rory Gilmore Qua 26 Jun 2019, 23:45
Da imagem temos:
AB = x
DB = 3x
DBFE é paralelogramo
O triângulo ADE é congruente ao triângulo GBF
O triângulo ABC é semelhante ao triângulo EPH
Dessas conclusões, obtemos EP = 2x
EH/AC = EP/AB
EH/AC = 2x/4x
EH/AC = 1/2
AB = x
DB = 3x
DBFE é paralelogramo
O triângulo ADE é congruente ao triângulo GBF
O triângulo ABC é semelhante ao triângulo EPH
Dessas conclusões, obtemos EP = 2x
EH/AC = EP/AB
EH/AC = 2x/4x
EH/AC = 1/2
Rory Gilmore- Monitor
- Mensagens : 1880
Data de inscrição : 28/05/2019
Localização : Yale University - New Haven, Connecticut
natanlopes_17 gosta desta mensagem
Tópicos semelhantes» (UFMG-97) Observe a figura.... semelhança de triângulos e triângulos retângulos.
» (UFMG) - Semelhança de triângulos e triângulos retângulos.
» Semelhança de Triângulos
» Semelhança de triângulos
» Semelhança de triângulos
» (UFMG) - Semelhança de triângulos e triângulos retângulos.
» Semelhança de Triângulos
» Semelhança de triângulos
» Semelhança de triângulos
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
