Semi-circunferências, arcos, tangentes externas...

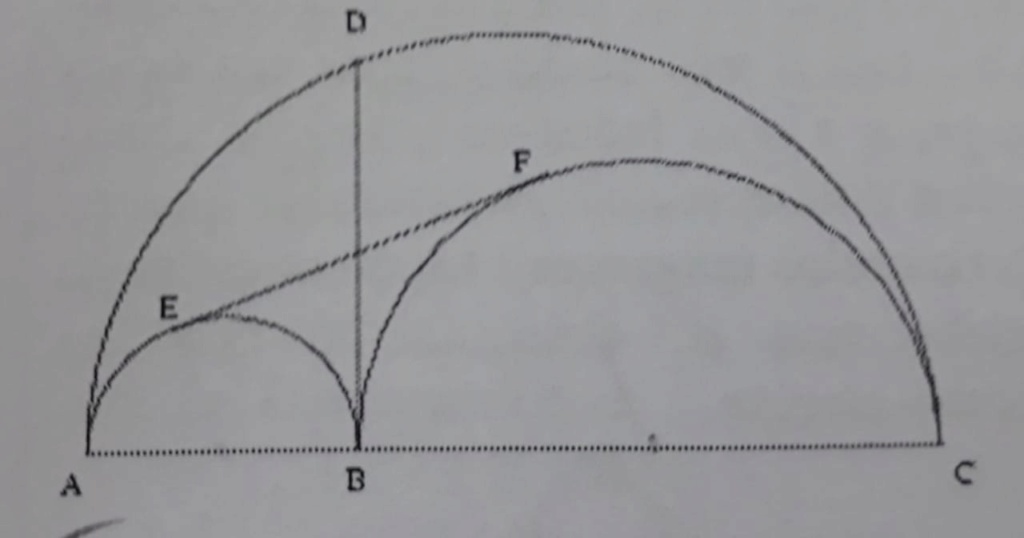
A conclusão (1) vem diretamente da média geométrica no semicírculo. Também pode ser obtida mediante relação métrica no triângulo retângulo ADC onde DB é sua altura em relação ao ângulo reto.

A conclusão (2) é aplicação de Pitágoras, conforme mostrado no desenho.

A conclusão (3) deriva da medida da tangente tirada por um ponto externo à circunferência.

De (1), (2) e (3) concluímos que BD = EF e que estes segmentos cortam-se ao meio. São, portanto, diagonais de um paralelogramo. É fácil ver que o ângulo interno E^BF deste paralelogramo é reto; logo, por simetria, todos os outros também o são. Portanto, EDFB é retângulo.

_____________________________________ EDIÇÃO

Embora seja muito fácil, nem precisa fazer considerações quanto àquele ângulo. O fato das diagonais terem mesma medida obriga a que o paralelogramo seja um retângulo.