Demonstre que:

por **Pietro di Bernadone** Sex 22 Jul 2011, 20:06

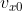Considere um movimento uniformemente acelerado genérico de uma partícula que se move ao longo do eixo OX. Nesse caso, a sua função-velocidade é escrita como $v_{x}=f_{x}(t)=v_{x0}+at$ , onde $v_{x0}$ é uma constante arbitrária (velocidade da partícula no instante t = 0) e $a$ é uma constante não-nula arbitrária (aceleração da partícula). 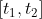Demonstre, nesse caso, que a velocidade média num intervalo de tempo qualquer $[t_{1},t_{2}]$ coincide não apenas com a velocidade instantânea no instante dado pela média aritmética dos instantes extremos do intervalo como também com a média aritmética das velocidades instantâneas nos extremos do intervalo. Em outras palavras, demonstre que $\left \langle f_{x} \right \rangle[t_{1},t_{2}]=f_{x}\left ( \frac{t_{1}+t_{2}}{2} \right )=\frac{f_{x}(t_{1})+f_{x}(t_{2})}{2}$ .

Se alguém puder me ajudar com a demostração ficarei muito agradecido. Por favor seja o mais detalhado possível.

Certo de sua atenção,

Pietro di Bernadone

por Quasar Sáb 23 Jul 2011, 20:51

Vc já postou uma questão parecida, lembra?

https://pir2.forumeiros.com/t15017-velocidade-instantanea

Demonstre que:

Demonstre que:

Re: Demonstre que:

Um fórum livre e democrático.