Trajetória

por **alansilva** Sáb 30 Mar 2019, 13:09

Com que velocidade inicial o jogador de basquetebol deve arremessar a bola, com ângulo $Trajetória Gif$ acima da horizontal, para converter o lance livre? As distâncias horizontais são $Trajetória Gif$ e $Trajetória Gif$ e as alturas são $Trajetória Gif$ e $Trajetória Gif$

Resposta: $Trajetória S$

por **DanMurray** Sáb 30 Mar 2019, 14:14

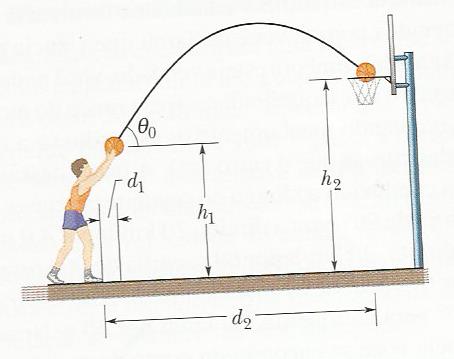
Analisando o movimento em x:

\\x_0=x+v_0\cos\theta\cdot t\\
d_2-d_1=v_0\cos\theta\cdot t\\\\
\boxed{t=\frac{\Delta x}{v_0\cos\theta}}

Analisando o movimento em y:

\\y=y_0+v_0\sin\theta\cdot t-\frac{gt^2}{2}\\\\
h_2=h_1+v_0\sin\theta\cdot t-\frac{gt^2}{2}\\\\
\Delta y=\frac{v_0\sin\theta\Delta x}{v_0\cos\theta}-\frac{g}{2}\cdot(\frac{\Delta x^2}{v_0^2\cos^2\theta})\\\\
\Delta y=\Delta x\tan\theta-\frac{g\Delta x^2}{2v_0^2\cos^2\theta}\\

\\2v_0^2\cos^2\theta\Delta y=2v_0^2\cos^2\theta\Delta x\tan\theta-g\Delta x^2\\\\2v_0^2\cos^2\theta(\Delta y-\Delta x\tan\theta)=-g\Delta x^2\\\\
2v_0^2\cos^2\theta(\Delta x\tan\theta - \Delta y)=g\Delta x^2\\\\
v_0=\sqrt{\frac{g\Delta x^2}{2\cos^2\theta(\Delta x\tan\theta - \Delta y)}}

Lembrando que g vale aproximadamente 32.17 ft/s^2.

Trajetória

Trajetória

Re: Trajetória

Um fórum livre e democrático.