Relações métricas num triãngulo qualquer

por Jrasilva Ter 19 Fev 2019, 18:48

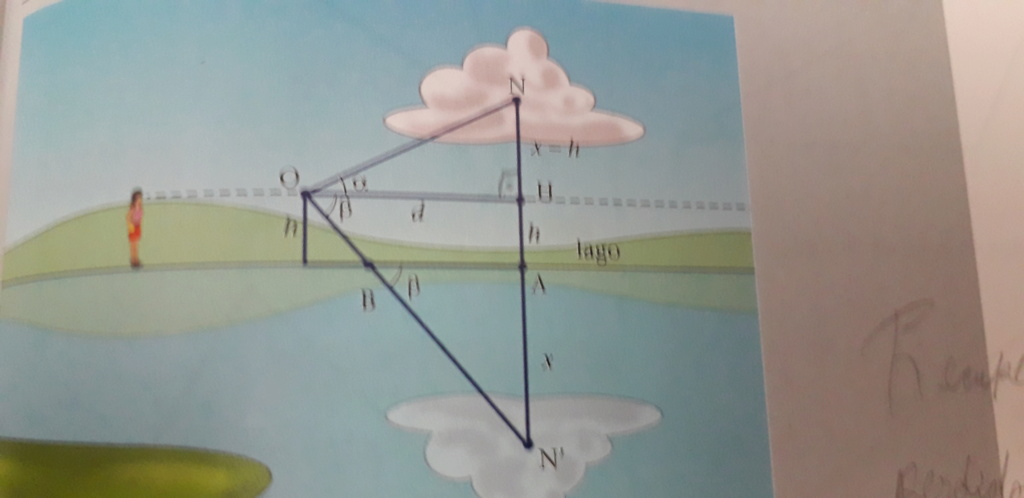
Um observador colocado nas margens de um lago, a uma altura h acima do nível da água, vê que o ângulo de uma nuvem é alfa, e o ângulo de depressão da imagem refletida sobre a água é Beta. Calcular a altura da nuvem.

Na segunda imagem está o gabarito que eu não entendi,não sei como usou proporções, solicito explicação.

Relações métricas num triãngulo qualquer 20190212

Relações métricas num triãngulo qualquer 20190213

por **Elcioschin** Ter 19 Fev 2019, 19:04

x = distância de N' à superfície = distância de N à superfície ---> x = NA' = NA

No triângulo retângulo OHN --> NH = x - h --> tgα = NH/OH --> tgα = (x - h)/d --> d = (x - h)/tgα --> I

No triângulo retângulo OHN' -> N'H = x + h -> tgβ = N'H/OH -> tgβ = (x + h)/d -> d = (x + h)/tgβ -> II

II = I ---> (x - h)/tgα = (x + h)/tgβ ---> x.tgβ - h.tgβ = x.tgα + h.tgα ---> x.tgβ - x.tgα = h.tgβ + h.tgα

x.(tgβ - tgα) = h.(tgβ + tgα) --> x = h.(tgβ + tgα)/(tgβ - tgα)

Relações métricas num triãngulo qualquer

Relações métricas num triãngulo qualquer

Re: Relações métricas num triãngulo qualquer

Um fórum livre e democrático.