Inequações e gráfico
4 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Inequações e gráfico
Inequações e gráfico
Considere o sistema de inequações:
\left\{\begin{matrix}
x^{2}+y^{2}-2x\geq 0\\
(x-1)^{2} + (y-\frac{\sqrt{3}}{2})^{2}\leq \frac{1}{4}
\end{matrix}\right.
a) Represente graficamente a solução desse sistema de inequações.
b) Calcule a área da superfície que representa a solução. (R=\frac{6\sqrt{3}-\pi}{24} unidades de área)
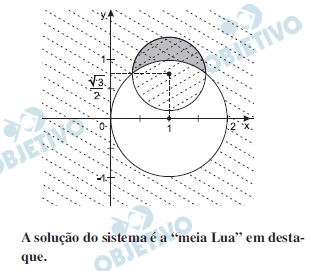
Dúvida: achei que a solução fosse a intersecção e não a meia-lua aqui representada no Objetivo: (peço que me expliquem)
x^{2}+y^{2}-2x\geq 0\\
(x-1)^{2} + (y-\frac{\sqrt{3}}{2})^{2}\leq \frac{1}{4}
\end{matrix}\right.
a) Represente graficamente a solução desse sistema de inequações.
b) Calcule a área da superfície que representa a solução. (R=
Dúvida: achei que a solução fosse a intersecção e não a meia-lua aqui representada no Objetivo: (peço que me expliquem)
Além dessa dúvida, eu gostaria de ajuda para resolver detalhadamente a letra b..
Última edição por ddmr0123 em Ter 11 Dez 2018, 13:48, editado 1 vez(es)

dd0123- Estrela Dourada

- Mensagens : 1362
Data de inscrição : 18/08/2018
Idade : 25
Localização : Brasil
 Re: Inequações e gráfico
Re: Inequações e gráfico
A área procurada é externa ao círculo maior e interna ao círculo menor: é a área Sm da meia lua escura
Para calcular a área, seja A e B os pontos de interseção das duas circunferências:
A(1/2, √3/2) ---> B(3/2, √3/2) ---> C(1, 0) ---> C'(1,√3/2)
Calcule a área Ss do segmento circular AC'BA do círculo maior:
Ss = S(setor CAB) - S(triângulo CAB)
Sm = (1/2).S(do círculo menor ) - Ss
Para calcular a área, seja A e B os pontos de interseção das duas circunferências:
A(1/2, √3/2) ---> B(3/2, √3/2) ---> C(1, 0) ---> C'(1,√3/2)
Calcule a área Ss do segmento circular AC'BA do círculo maior:
Ss = S(setor CAB) - S(triângulo CAB)
Sm = (1/2).S(do círculo menor ) - Ss

Elcioschin- Grande Mestre

- Mensagens : 73179
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Inequações e gráfico
Re: Inequações e gráfico
Obrigado, sr. Elcio!
Só estou com mais uma dúvida: como é que eu iria saber que o exercício quer a área externa ao círculo maior e não a interna? Possui ligação com as inequações?
Só estou com mais uma dúvida: como é que eu iria saber que o exercício quer a área externa ao círculo maior e não a interna? Possui ligação com as inequações?

dd0123- Estrela Dourada

- Mensagens : 1362
Data de inscrição : 18/08/2018
Idade : 25
Localização : Brasil
 Re: Inequações e gráfico
Re: Inequações e gráfico
Sim.
x²+y²≤R²: hachura a parte interna.
x²+y²≥R²: hachura a parte externa.
É só você pensar no seguinte: a inequação x²+y²≤R² nos sugere o seguinte: qual é o par ordenado (x,y) tal que a soma dos quadrados das coordenadas é menor ou igual a raio ao quadrado? Por isso hachuramos a parte interna, pois neste caso só os pares ordenados internos e contidos (pois a desigualdade é menor ou igual) na circunferência satisfazem o que foi sugerido. Para a inequação x²+y²≥R² a ideia é a mesma. A única diferença agora é que queremos todos os pares ordenados tais que a soma dos quadrados das coordenadas seja maior ou igual ao raio ao quadrado. O que satisfaz isso são os pares localizados na região externa à circunferência, bem como os pares ordenados situados sobre a circunferência (pois a desigualdade é maior ou igual). Caso tivéssemos a situação x²+y²>R², a circunferência deveria ser tracejada para indicar que os pontos contidos na circunferência não fazem parte da solução, afinal, para todo (x,y) ∈ x²+y²>R² tem-se x²+y²=R² e para x²+y²>R² queremos apenas os pares (x,y) tais que a soma dos quadrados das coordenadas seja maior que o quadrado do raio.
Caso tenha ficado confuso, é só falar que eu tento melhorar a explicação.
x²+y²≤R²: hachura a parte interna.
x²+y²≥R²: hachura a parte externa.
É só você pensar no seguinte: a inequação x²+y²≤R² nos sugere o seguinte: qual é o par ordenado (x,y) tal que a soma dos quadrados das coordenadas é menor ou igual a raio ao quadrado? Por isso hachuramos a parte interna, pois neste caso só os pares ordenados internos e contidos (pois a desigualdade é menor ou igual) na circunferência satisfazem o que foi sugerido. Para a inequação x²+y²≥R² a ideia é a mesma. A única diferença agora é que queremos todos os pares ordenados tais que a soma dos quadrados das coordenadas seja maior ou igual ao raio ao quadrado. O que satisfaz isso são os pares localizados na região externa à circunferência, bem como os pares ordenados situados sobre a circunferência (pois a desigualdade é maior ou igual). Caso tivéssemos a situação x²+y²>R², a circunferência deveria ser tracejada para indicar que os pontos contidos na circunferência não fazem parte da solução, afinal, para todo (x,y) ∈ x²+y²>R² tem-se x²+y²=R² e para x²+y²>R² queremos apenas os pares (x,y) tais que a soma dos quadrados das coordenadas seja maior que o quadrado do raio.
Caso tenha ficado confuso, é só falar que eu tento melhorar a explicação.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8546
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Inequações e gráfico
Re: Inequações e gráfico
Algumas imagens.
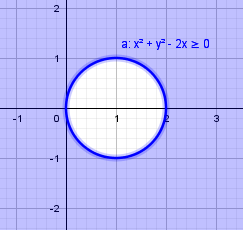
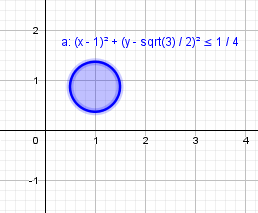
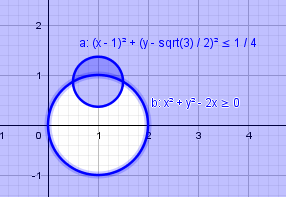
Intersecção entre as regiões (região que nos interessa e que está pintada de forma mais intensa.):
A segunda fase da FUVEST de 2014 tem uma questão linda sobre esse assunto. Está na página 2 e é a questão 2.
http://www.curso-objetivo.br/vestibular/resolucao_comentada/fuvest/2014_2fase/3dia/fuvest2014_2fase_3dia_prova.pdf
Ela não é muito difícil. Com paciência ela sai "tranquilamente". Tente fazer.
Duas resoluções:
http://www.curso-objetivo.br/vestibular/resolucao_comentada/fuvest/fuvest2014_2fase.asp
https://www.youtube.com/watch?v=nClKs_RsmSs


Intersecção entre as regiões (região que nos interessa e que está pintada de forma mais intensa.):

A segunda fase da FUVEST de 2014 tem uma questão linda sobre esse assunto. Está na página 2 e é a questão 2.
http://www.curso-objetivo.br/vestibular/resolucao_comentada/fuvest/2014_2fase/3dia/fuvest2014_2fase_3dia_prova.pdf
Ela não é muito difícil. Com paciência ela sai "tranquilamente". Tente fazer.
Duas resoluções:
http://www.curso-objetivo.br/vestibular/resolucao_comentada/fuvest/fuvest2014_2fase.asp
https://www.youtube.com/watch?v=nClKs_RsmSs
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8546
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Inequações e gráfico
Re: Inequações e gráfico
Finalmente entendi!!! Valeu mesmo, Giovana! Resposta mais que completa! 


dd0123- Estrela Dourada

- Mensagens : 1362
Data de inscrição : 18/08/2018
Idade : 25
Localização : Brasil
 Re: Inequações e gráfico
Re: Inequações e gráfico
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8546
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Inequações e gráfico
Re: Inequações e gráfico
Genial mesmo! Obrigado novamente

dd0123- Estrela Dourada

- Mensagens : 1362
Data de inscrição : 18/08/2018
Idade : 25
Localização : Brasil
 Re: Inequações e gráfico
Re: Inequações e gráfico
Excelente didática têm as suas explicações, Giovana...
wadekly- Jedi

- Mensagens : 218
Data de inscrição : 29/03/2024
 Re: Inequações e gráfico
Re: Inequações e gráfico
wadekly escreveu:Excelente didática têm as suas explicações, Giovana...
Muito obrigada!
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8546
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Tópicos semelhantes
Tópicos semelhantes» Grafico de sistema de inequações
» Inequações de 2º grau e Inequações Produto
» Inequações
» Inequações
» Inequações b)
» Inequações de 2º grau e Inequações Produto
» Inequações
» Inequações
» Inequações b)
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos