Geometria plana - área

O piso de uma sala tem a forma de um quadrado ABCD com lado 7m. Esse piso será revestido de forma que as áreas marcadas fiquem cinza e o resto, branco. Os pontos E, F, G e H são vértices de outro quadrado menor e foram posicionados a 3 m do ponto B, A, D e C, respectivamente. Já os pontos I, J, K e L são pontos médios dos lados do quadrado EFGH. 

A área cinza mede: 


A) 30 metros quadrados 
B)29 metros quadrados 
C)28 metros quadrados 
D)25 metros quadrados 
E) 24 metros quadrados

Meu problema consiste em achar o lado do quadrado central ou então excluí-lo a partir da área branca. Agradeço a ajuda! Sei que o lado do quadrado branco é 5m, mas não consigo prosseguir para calcular as áreas dos 4 triângulos brancos.

Veja a questão e resposta nesse link, acredito que dai vc consegue responder sua dúvida.

https://pir2.forumeiros.com/t153190-area-de-quadrilatero-hachurado

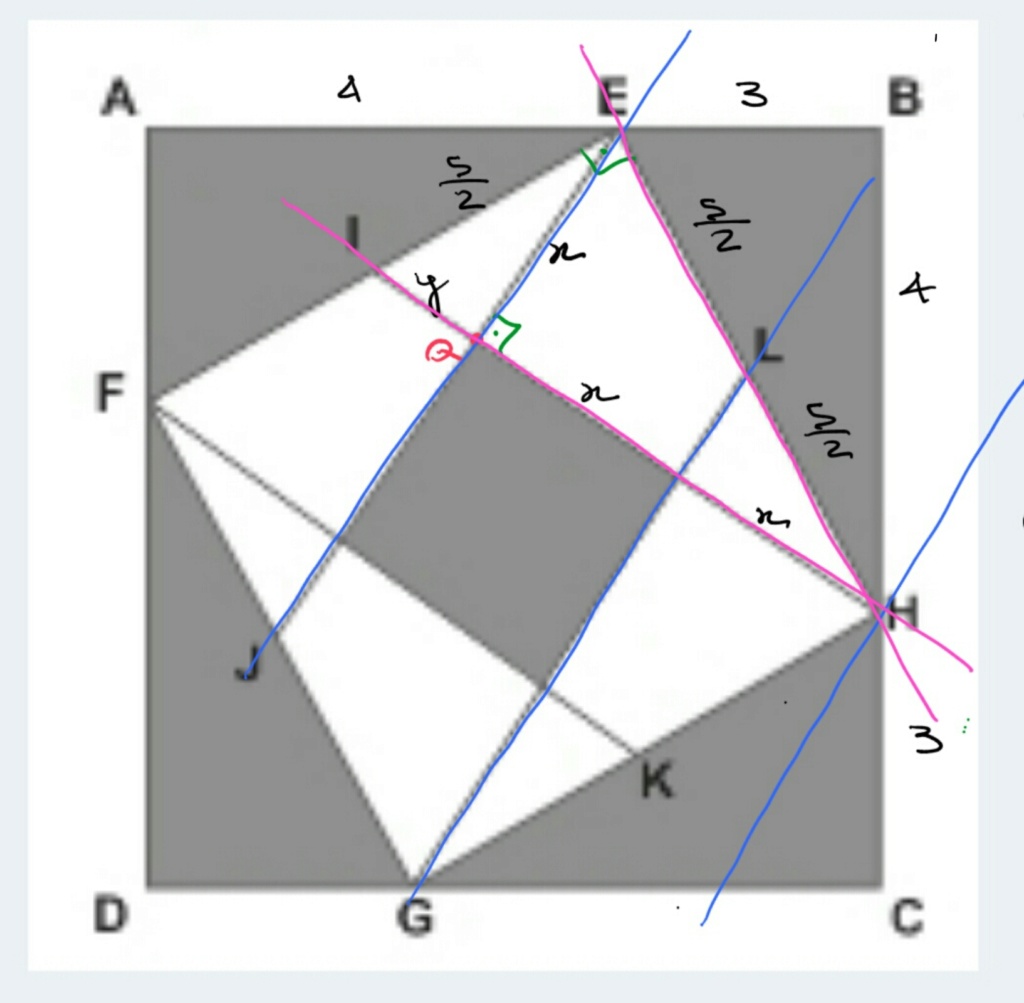
Considere o triângulo EBH. É reto e por Pitágoras sabemos que EH = 5. Também, como L é ponto médio de EH temos que EL=LH=5/2.

Considere, agora, as concorrentes violetas cortadas pelas paralelas azuis. Pelo teorema de Tales concluímos que são iguais os segmentos anotados no desenho como x; chamamos de y ao segmento menor que completa o segmento HI.

Note que o triângulo EHI é reto e que EJ \perp HI.

Por Pitágoras no triâng. EHI,
\\ 2x+y = \sqrt{\frac{25}{4} + 25} \,\,\longrightarrow \,\, 2x+y = \frac{5}{2}\sqrt{5} \,\,\,\,\,\,\, (1)

área do triâng. EHI:
\\ \frac{\overline{EI}\cdot \overline{EH}}{2} = \frac{\overline{HI}\cdot \overline{QE}}{2} \,\,\rightarrow\,\, \frac{5}{2}\cdot 5 = (2x+y)\cdot x \,\,\,\,\,\,\, (2)

(1) em (2) -----> \frac{25}{2} = \frac{5}{2}\sqrt{5}\cdot x \,\,\, \longrightarrow \,\,\, x=\sqrt{5}

Portanto, lembrando que a área cinza (S) contém quatro triângulos congruentes ao EBH mais o quadrado pequeno de lado x, temos:
\\ S = 4 \cdot \frac{3 \cdot 4}{2} + x^{2} = 24 + \left (\sqrt{5}  \right )^{2} \,\,\, \longrightarrow \,\,\, \boxed{\,\,S=29 \,\, m^2\,\,}