Ângulos em um triângulo

Considere a figura a seguir e determine o valor de x, em graus.




Obs.: Não tenho o gabarito! :-(

A Regra IX do fórum não permite links.
EDIT colando a figura conforme tutorial para postagem de imagens (na 1ª página do fórum)

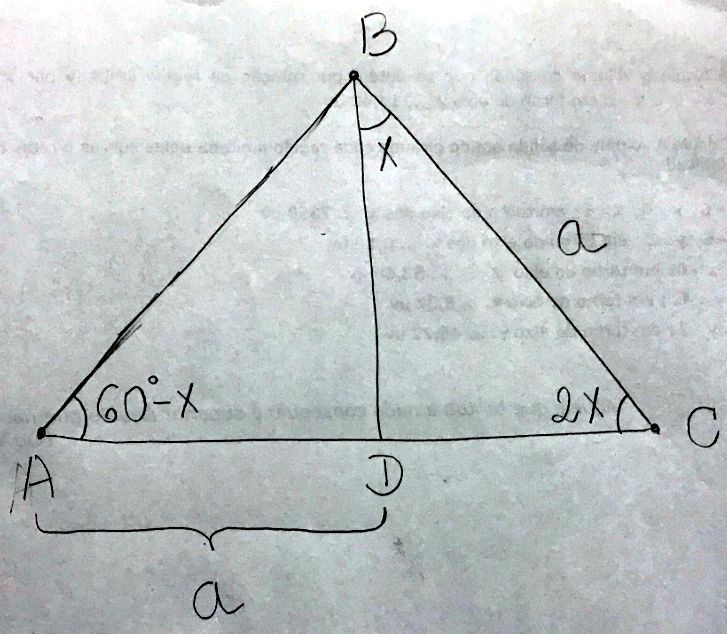
Seja h = AD

B^DC  = 180º - x - 2.x ---> B^DC = 180º - 3.x ---> sen(B^DC) = sen(3.x) --->

sen(B^DC) = 3.senx - 4.sen³x

No ângulo raso ADC ---> A^DB = 3.x ---> sen(3.x) = 3.senx - 4.sen³x

No triângulo ABD ---> A^BD = 180º - A^DB - BÂD ---> A^BD = 180º - 3.x - (60º - x) --->

A^BD = 120º - 2.x ---> sen(A^BD) = sen(120º - 2.x) --->

sen(A^DB) = (√3/2).cos(2.x) + (1/2).sen(2.x) ---> cos(2.x) = 2.cos²x - 1 = 1 - 2.sen²x --->

sen(2.x) = 2.senx.cosx

sen(60º - x) = (√3/2).cosx - (1/2).senx

Lei dos senos:

1) No ∆ ABD ---> BD/sen(BÂC) = AD/sen(A^BD) ---> h/sen(60º - x) = a/sen(120º - 2.x)

2) No ∆ CBD ---> BD/sen(B^CD) = CD/sen(C^BD) ---> h/sen(2.x) = a/sen(180º - 3.x)

Complete