(Rússia - Geometria)

Dados três pontos A, B, C , sobre uma reta l , são construídos triângulos equiláteros  ABC_{1} \ e \ BCA_{1}  em um mesmo semi-plano com respeito à l . Se M, N são os pontos médios de AA_{1}, CC_{1} , respectivamente, mostre que \triangle BMN é equilátero.

Olá ,
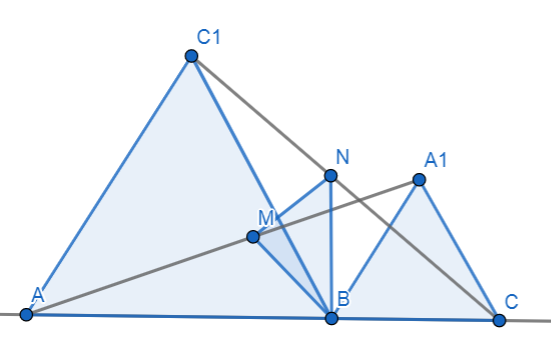
Inicialmente ligando C1A1 , formamos o triângulo C1BA1 , de tal forma que o ângulo B desse triângulo seja 60 graus , repare que como a reta é linear a soma dos três angulos de cada triângulo deve dar 180 graus , como os triângulos ABC1 e A1BC são equiláteros seus ângulos internos são iguais a 60 graus , logo necessariamente para completar 180 graus , o ângulo dito é realmente 60 graus.

Agora analisando os triângulos ABA1 e CBC1 , perceba que eles são congruentes pelo caso LAL (lado ângulo lado) , perceba que ambos possuem um lado em cada triângulo equilátero.Para perceber que o ângulo B de ABA1 e o ângulo B de CBC1 são iguais , perceba que ambos são iguais a 120 , pois tem a soma de 60 graus proporcionado por cada triângulo equilatero e mais 60 graus do ângulo B do triângulo C1BA1 , portanto ABA1 e CBC1 são congruentes.
Então considerando esses dois triângulos que são congruentes perceba tais relações abaixo:
A=C1 
C=A1 
B=B ( de cada triângulo)

Como os triângulos são congruentes , os mesmo expostos acima , perceba que C1C=AA1 , dessa maneira é considerando os pontos médios de tais segmentos (M e N) , temos :

AM=MA1=CN=NC1

Com isso vamos observar dois triângulos agora , o triângulo formado por A1MB e o triângulo formado por CBN , perceba que ambos são congruentes pelo também caso LAL (lado angulo lado) como exposto no caso de congruência dos triângulos lá em cima apresentado tiramos a conclusão de que C=A1 , como desta congruência tiramos que A1M=CN e como ambos triângulos possuem um lado no menor triângulo equilatero são então triângulos congruentes , logo concluímos que NB=MB.

Agora voltando a relação de congruência dos triângulos ABA1 e C1BC temos que se mantermos o triângulo C1BC e rotacionarmos o triângulo ABA1 em 60 graus no sentido horário A1 inicialmente irá conciliar com C , assim como A conciliara com C1 e M conciliara com N , pois são triângulos congruentes.
Logo M rotaciona 60 graus para conciliar com o ponto N , dessa maneira o ângulo B do triângulo MNB é 60 graus.
Como o triângulo  e isosceles , pois NB=BM , e o ângulo de B é 60 graus , o triângulo terá seus três angulos iguais a 60 e seus lados serão iguais, logo o triângulo MNB é equilatero.

Sei que sua dúvida já foi respondida, mas se ainda precisar, nesse vídeo do POTI, a partir do minuto 41:50 tem a resolução da mesma questão:

https://www.youtube.com/watch?v=fZLIdkqp-jk

^^