Função bijetora - FME
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Re: Função bijetora - FME
Re: Função bijetora - FME
Boa noite, acho que posso te ajudar. Tentei deixar bem moidinho.
Para facilitar vou representar a raiz quadrada por raizV
Para essa função ser bijetora ela deve ser:
1) Injetora;
2) Sobrejetora;
Passo 1:
Vamos começar pela injeção:
Vamos pegar dois números reais quaisquer a e b de ta modo que eles façam parte do domínio de f(x), e a < b.
Portanto temos: 0 < a < b < s.
Para garantirmos que f(x) é injetora, f( a ) < f( b ) para todo a < b, tal que 0 < a < b < s.
Vamos fazer algumas manipulações, tendo sempre em mente que a < b são positivos:
1) a < b então -a > -b;
2) -a > -b então somando "s" a ambos os lados temos s-a > s-b;
3) s-a > s-b pode ser elevado a -1: 1/(s-a) < 1/(s-b);
4) a < b < s elevando a -1: 1/a > 1/( b ) > 1/s;
5) 1/a > 1/( b ) então -1/a < -1/( b );
Repare nas trocas de sinais e na inversão do sinal de inequação toda vez que realizamos contas de -1 e de inversão(^-1).
Aqui tenho que fazer um parênteses no exercício. Deve-se ter atenção no conjunto em que se está trabalhando, pois isso só é possível pois temos a garantia de que 0
3 > -2 temos que multiplicando por -1: -3 < 2 o que é verdade, e independe do conjunto trabalhado pelo que eu sei. Porém:
3 > -2 ao inverter-se temos que 1/3 <-1/2 é um absurdo matemático. Quando inverte-se deve atentar para esse fato.
Voltando:
Se somarmos as conclusões 3) e 5), temos:
1/(s-a) - 1/a < 1/(s-b) - 1/b;
Repare que simplificando as subtrações em ambos os lados, podemos escrever (2a-s)/a(s-a) e (2b-s)/b(s-b), que é exatamente a mesma coisa que f(a) e f(b).
----Outro modo: Frações parciais.
Poderíamos ter logo no começo do exercício ter aplicado a e b em f(x) e desmembra-la em frações parciais:
Ex:
f(a)=(2a-s)/a(s-a) = M/a + N/(s-a).
Efetuando as contas: M = (2*0 - s)/(s - 0) = -1;
N = (2*s - s)/(s) = 1;
f(a)= 1/(s-a) - 1/a. O mesmo pode ser feito para f(x) com x =b.
Enfim, chegamos a conclusão de que a e b pertencentes ao domínio de f(x), são tais que para qualquer a < b temos f( a ) < f ( b ). Logo, a função é injetora.
Passo 2 sobrejeção:
Vamos encontrar os pontos em que ela não está definida. x=0 e x=s. Porém eles não fazem parte do domínio, então não podemos afirmar que a função é sobrejetora, mas também não podemos afirmar o contrário, então vamos continuar tentando.
Explicação: Para facilitar a compreensão. Veja que pode ser que o a imagem seja só os reais positivos, enquanto que o contra-domínio são todos os reais. Precisamos garantir que dado um y qualquer, haverá um x no domínio, tal que f(x)=y.
Vamos lá. Primeira coisa vamos achar a função inversa.
Vamos chegar em um dado momento das contas a -y².x + (sy - 2).x - s=0 ou y².x + (2 - sy)x + s=0.
Podemos resolver usando Baskhara(acho que é assim que se escreve).
∆=s²y²+4, ou seja ∆ > 0 para qualquer y que a gente pegue.
^2+4ys}}{2y})
 (Redundância: Se um crashar tem outra). OBS: As duas são de sites diferentes.
(Redundância: Se um crashar tem outra). OBS: As duas são de sites diferentes.



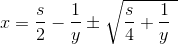








Caso as três imagens(de sites diferentes) crashem: https://2img.net/h/oi66.tinypic.com/20jr2g5.jpg tem um 4º aqui.
ERRATA IMPORTANTE: Nas quatro imagens está somente s/4 dentro da raiz quando o correto é s²/4.
Achando x1 e x2:
x1 = s/2 -1/y + raizV(s²/4 + 1/y²) e x2 = s/2 -1/y - raizV(s²/4 + 1/y²).
Veja que joguei o denominador 2y para dentro da raiz.
Perceba que (s/2 - 1/y)² = s²/4 + 1/y² - s/y. Perceba que a raiz quadrada dessa expressão é:
1)raizV(s²/4 + 1/y² - s/y). Comparando com 2)raizV(s²/4 + 1/y²), temos que 1 pode ser maior que a 2 ou menor, e isso depende do elemento -s/y na raiz. Como s > 0, se y > 0 -s/y < 0 e então 1 será menor que 2.
Mas se y < 0, -s/y > 0. Como temos que x tem que ser positivo, basta perceber que se pegarmos um y < 0, teremos que a função inversa é x2, e se tomarmos y > 0, temos que a função inversa é x1.
Logo, independentemente do y pego, seja ele maior ou menor que zero. Mas perceba que elas não cobrem o caso y=0. Vamos calcular aplicando f(x)=0. Achamos que x tem que ser x=s/2. Mas 0 < s/2 < s, logo, temos um x em 0 < x < s para qualquer y que tomarmos nos reais, ou seja, o conjunto dos reais é a imagem, e como os reais são o contra-domínio, a função é sobrejetora.
Logo a função é bijetora. Espero ter ajudado. Qualquer dúvida tamo ai.
Para facilitar vou representar a raiz quadrada por raizV
Para essa função ser bijetora ela deve ser:
1) Injetora;
2) Sobrejetora;
Passo 1:
Vamos começar pela injeção:
Vamos pegar dois números reais quaisquer a e b de ta modo que eles façam parte do domínio de f(x), e a < b.
Portanto temos: 0 < a < b < s.
Para garantirmos que f(x) é injetora, f( a ) < f( b ) para todo a < b, tal que 0 < a < b < s.
Vamos fazer algumas manipulações, tendo sempre em mente que a < b são positivos:
1) a < b então -a > -b;
2) -a > -b então somando "s" a ambos os lados temos s-a > s-b;
3) s-a > s-b pode ser elevado a -1: 1/(s-a) < 1/(s-b);
4) a < b < s elevando a -1: 1/a > 1/( b ) > 1/s;
5) 1/a > 1/( b ) então -1/a < -1/( b );
Repare nas trocas de sinais e na inversão do sinal de inequação toda vez que realizamos contas de -1 e de inversão(^-1).
Aqui tenho que fazer um parênteses no exercício. Deve-se ter atenção no conjunto em que se está trabalhando, pois isso só é possível pois temos a garantia de que 0
3 > -2 temos que multiplicando por -1: -3 < 2 o que é verdade, e independe do conjunto trabalhado pelo que eu sei. Porém:
3 > -2 ao inverter-se temos que 1/3 <-1/2 é um absurdo matemático. Quando inverte-se deve atentar para esse fato.
Voltando:
Se somarmos as conclusões 3) e 5), temos:
1/(s-a) - 1/a < 1/(s-b) - 1/b;
Repare que simplificando as subtrações em ambos os lados, podemos escrever (2a-s)/a(s-a) e (2b-s)/b(s-b), que é exatamente a mesma coisa que f(a) e f(b).
----Outro modo: Frações parciais.
Poderíamos ter logo no começo do exercício ter aplicado a e b em f(x) e desmembra-la em frações parciais:
Ex:
f(a)=(2a-s)/a(s-a) = M/a + N/(s-a).
Efetuando as contas: M = (2*0 - s)/(s - 0) = -1;
N = (2*s - s)/(s) = 1;
f(a)= 1/(s-a) - 1/a. O mesmo pode ser feito para f(x) com x =b.
Enfim, chegamos a conclusão de que a e b pertencentes ao domínio de f(x), são tais que para qualquer a < b temos f( a ) < f ( b ). Logo, a função é injetora.
Passo 2 sobrejeção:
Vamos encontrar os pontos em que ela não está definida. x=0 e x=s. Porém eles não fazem parte do domínio, então não podemos afirmar que a função é sobrejetora, mas também não podemos afirmar o contrário, então vamos continuar tentando.
Explicação: Para facilitar a compreensão. Veja que pode ser que o a imagem seja só os reais positivos, enquanto que o contra-domínio são todos os reais. Precisamos garantir que dado um y qualquer, haverá um x no domínio, tal que f(x)=y.
Vamos lá. Primeira coisa vamos achar a função inversa.
Vamos chegar em um dado momento das contas a -y².x + (sy - 2).x - s=0 ou y².x + (2 - sy)x + s=0.
Podemos resolver usando Baskhara(acho que é assim que se escreve).
∆=s²y²+4, ou seja ∆ > 0 para qualquer y que a gente pegue.
 (Redundância: Se um crashar tem outra). OBS: As duas são de sites diferentes.
(Redundância: Se um crashar tem outra). OBS: As duas são de sites diferentes.
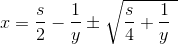






Caso as três imagens(de sites diferentes) crashem: https://2img.net/h/oi66.tinypic.com/20jr2g5.jpg tem um 4º aqui.
ERRATA IMPORTANTE: Nas quatro imagens está somente s/4 dentro da raiz quando o correto é s²/4.
Achando x1 e x2:
x1 = s/2 -1/y + raizV(s²/4 + 1/y²) e x2 = s/2 -1/y - raizV(s²/4 + 1/y²).
Veja que joguei o denominador 2y para dentro da raiz.
Perceba que (s/2 - 1/y)² = s²/4 + 1/y² - s/y. Perceba que a raiz quadrada dessa expressão é:
1)raizV(s²/4 + 1/y² - s/y). Comparando com 2)raizV(s²/4 + 1/y²), temos que 1 pode ser maior que a 2 ou menor, e isso depende do elemento -s/y na raiz. Como s > 0, se y > 0 -s/y < 0 e então 1 será menor que 2.
Mas se y < 0, -s/y > 0. Como temos que x tem que ser positivo, basta perceber que se pegarmos um y < 0, teremos que a função inversa é x2, e se tomarmos y > 0, temos que a função inversa é x1.
Logo, independentemente do y pego, seja ele maior ou menor que zero. Mas perceba que elas não cobrem o caso y=0. Vamos calcular aplicando f(x)=0. Achamos que x tem que ser x=s/2. Mas 0 < s/2 < s, logo, temos um x em 0 < x < s para qualquer y que tomarmos nos reais, ou seja, o conjunto dos reais é a imagem, e como os reais são o contra-domínio, a função é sobrejetora.
Logo a função é bijetora. Espero ter ajudado. Qualquer dúvida tamo ai.
Última edição por Mbssilva em Sex 05 Jan 2018, 22:40, editado 1 vez(es)
____________________________________________
Baixe o livro Análise Combinatória e Probabilidade do A.C. Morgado com o gabarito e o solucionário dos exercícios.
Link 1: https://drive.google.com/open?id=0B4rrFzh6MB34NlVpeEpMZEdYSWs
Link 2: https://mega.nz/#F!FcpEWTCC!XrlsFKcPNR3ePOFm3OVJsg
Mbssilva- Elite Jedi

- Mensagens : 359
Data de inscrição : 15/01/2015
Idade : 25
Localização : Paraná, Brasil
 Re: Função bijetora - FME
Re: Função bijetora - FME
Boa tarde. Agora eu estava olhando a resolução novamente, e percebi que não mostrei que x1 e x2 serão menores que s para qualquer y que tomarmos nos reais.
Se: y>0 fˉ¹(x)=x1
y<0 fˉ¹(x)=x2
Repare que se o x que encontrarmos fosse maior que s, a diferença s - x seria menor que 0.
Então vou adicionar s aos dois lados de x1:
s - x1 = s/2 + 1/y - raizV( s²/4 + 1/y² )
Veja que como y>0 para fˉ¹(x)=x1 então s - x1 = x2 > 0, por que x2 é maior que 0 e s - x1 é igual a x2.
Perceba a semelhança entre as expressões, a diferença é unicamente o sinal na frente do 1/y. Mas como o y<0 na expressão x2, então, na hora que aplicarmos teríamos: x2 = s/2 + 1/|y| - raizV( s²/a + 1/y² ), que é igual a s - x1, pois |y|=y se y>0, então s - x1 = s/2 + 1/|y| - raizV( s²/a + 1/y² ) = x2 > 0.
Se fizer o mesmo raciocínio para s - x2, verá que s - x2 = x1 > 0.
Agora sim. Espero ter ajudado.
Se: y>0 fˉ¹(x)=x1
y<0 fˉ¹(x)=x2
Repare que se o x que encontrarmos fosse maior que s, a diferença s - x seria menor que 0.
Então vou adicionar s aos dois lados de x1:
s - x1 = s/2 + 1/y - raizV( s²/4 + 1/y² )
Veja que como y>0 para fˉ¹(x)=x1 então s - x1 = x2 > 0, por que x2 é maior que 0 e s - x1 é igual a x2.
Perceba a semelhança entre as expressões, a diferença é unicamente o sinal na frente do 1/y. Mas como o y<0 na expressão x2, então, na hora que aplicarmos teríamos: x2 = s/2 + 1/|y| - raizV( s²/a + 1/y² ), que é igual a s - x1, pois |y|=y se y>0, então s - x1 = s/2 + 1/|y| - raizV( s²/a + 1/y² ) = x2 > 0.
Se fizer o mesmo raciocínio para s - x2, verá que s - x2 = x1 > 0.
Agora sim. Espero ter ajudado.
____________________________________________
Baixe o livro Análise Combinatória e Probabilidade do A.C. Morgado com o gabarito e o solucionário dos exercícios.
Link 1: https://drive.google.com/open?id=0B4rrFzh6MB34NlVpeEpMZEdYSWs
Link 2: https://mega.nz/#F!FcpEWTCC!XrlsFKcPNR3ePOFm3OVJsg
Mbssilva- Elite Jedi

- Mensagens : 359
Data de inscrição : 15/01/2015
Idade : 25
Localização : Paraná, Brasil
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












