Condição para tensão mínima

por **Davi Paes Leme** Ter 05 Set 2017, 15:30

Um corpo de massa m é arrastado sobre uma cunha com inclinação α por um fio que faz um ângulo β com a superfície da mesma. O coeficiente de atrito entre o corpo e a cunha é μ. Calcule o valor de β de tal modo que a tensão no fio seja mínima.

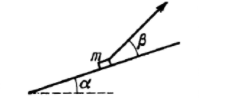
Calculei a tensão e encontrei: T= mg(senα + μ.cosα)/cosβ - μ.senβ
Daí, para que a tensão seja mínima o denominador terá que ser máximo.
Mas como consigo esse valor de beta?

por **JoaoGabriel** Qui 07 Set 2017, 11:54

(b = beta e u = mu)

Cara, eu fiz aqui e achei o denominador como cos(b) + u*sin(b). Chame este denominador de f(b). Queremos o máximo de f(b), portanto:

d(f(b))/db = 0 --> -sin(b) + u*cos(b) = 0 --> u*cos(b) = sin(b) --> sin(b)/cos(b) = u --> tan(b) = u --> b = arctan(u)

Pode até fazer o teste da derivada segunda para garantir que o ponto é de máximo:

d''f(b) = -cos(b) -u*sin(b), substitua b por atan(u) e efetue a álgebra.