A área
2 participantes
Página 1 de 1
A área
por RamonLucas Sex 21 Jul 2017, 19:43
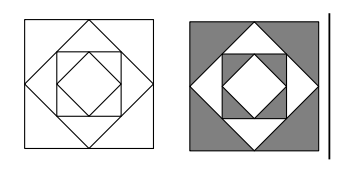
A figura representa 4 quadrados de uma sequência de 8 quadrados construídos de tal forma que o primeiro quadrado (o maior deles) tem lado igual à 1u.c., e cada quadrado, a partir do segundo, tem seus vértices nos pontos médios dos lados do quadrado anterior. Considerando-se a área da região que se encontra no interior do primeiro quadrado e no exterior do segundo, e a área no interior do terceiro quadrado e no exterior do quarto, e assim por diante, pode-se concluir que a soma de todas essas áreas é igual, em u.a., a:
a) 171/256 b) 85/128 c) 43/64 d) 21/32 e) 11/16
RamonLucas- Estrela Dourada
- Mensagens : 2034
Data de inscrição : 26/03/2015
Idade : 31
Localização : Brasil, Búzios.
Re: A área
por EsdrasCFOPM Sex 21 Jul 2017, 21:00
Os lados decrescem em uma P.G. de q=√2/2 e as áreas em q'=1/2.
l1=1 --> A1=1
l2=√2/2 --> A2=1/2
l3=1/2 --> A3=1/4
l4=√2/4 --> A4=1/8
Como é uma sequência de 8 quadrados continua até l8.
l5=1/4 --> A1=1/16
l6=√2/8 --> A2=1/32
l7=1/8 --> A3=1/64
l8=√2/16 --> A4=1/128
Área=A1-A2+A3-A4+A5-A6+A7-A8
Área=1-1/2+1/4-1/8+1/16-1/32+1/64-1/128
Área=128/128-64/128+32/128-16/128+8/128-4/128+2/128-1/128
Área=85/128
l1=1 --> A1=1
l2=√2/2 --> A2=1/2
l3=1/2 --> A3=1/4
l4=√2/4 --> A4=1/8
Como é uma sequência de 8 quadrados continua até l8.
l5=1/4 --> A1=1/16
l6=√2/8 --> A2=1/32
l7=1/8 --> A3=1/64
l8=√2/16 --> A4=1/128
Área=A1-A2+A3-A4+A5-A6+A7-A8
Área=1-1/2+1/4-1/8+1/16-1/32+1/64-1/128
Área=128/128-64/128+32/128-16/128+8/128-4/128+2/128-1/128
Área=85/128
EsdrasCFOPM- Estrela Dourada
- Mensagens : 1247
Data de inscrição : 22/02/2016
Idade : 30
Localização : Salvador, Bahia, Brasil
Re: A área
por RamonLucas Sex 21 Jul 2017, 22:16
EsdrasCFOPM escreveu:Os lados decrescem em uma P.G. de q=√2/2 e as áreas em q'=1/2.
l1=1 --> A1=1
l2=√2/2 --> A2=1/2
l3=1/2 --> A3=1/4
l4=√2/4 --> A4=1/8
Não entendi o destacado acima. Como fez para descobrir a razão ?
RamonLucas- Estrela Dourada
- Mensagens : 2034
Data de inscrição : 26/03/2015
Idade : 31
Localização : Brasil, Búzios.
Re: A área
por EsdrasCFOPM Sex 21 Jul 2017, 22:30
Usando a fórmula de Pitágoras. Como o lado de Qn vai ser igual a diagonal de Qn+1, basta analisar o que acontece que você chega nas conclusões sobre as razões.
(1)2=(l2)2+(l2)2
l2=√2/2
(√2/2)2=(l3)2+(l3)2
2(l3)2=2/4
(l3)2=1/4
l3=1/2
(1/2)2=(l4)2+(l4)2
(l4)2=1/8
l4=1/2√2
l4=√2/4
(1)2=(l2)2+(l2)2
l2=√2/2
(√2/2)2=(l3)2+(l3)2
2(l3)2=2/4
(l3)2=1/4
l3=1/2
(1/2)2=(l4)2+(l4)2
(l4)2=1/8
l4=1/2√2
l4=√2/4
EsdrasCFOPM- Estrela Dourada
- Mensagens : 1247
Data de inscrição : 22/02/2016
Idade : 30
Localização : Salvador, Bahia, Brasil
Re: A área
por RamonLucas Sex 21 Jul 2017, 22:54
Entendi, perfeitamente.Muito obrigado.EsdrasCFOPM escreveu:Usando a fórmula de Pitágoras. Como o lado de Qn vai ser igual a diagonal de Qn+1, basta analisar o que acontece que você chega nas conclusões sobre as razões.
(1)2=(l2)2+(l2)2
l2=√2/2
(√2/2)2=(l3)2+(l3)2
2(l3)2=2/4
(l3)2=1/4
l3=1/2
(1/2)2=(l4)2+(l4)2
(l4)2=1/8
l4=1/2√2
l4=√2/4
RamonLucas- Estrela Dourada
- Mensagens : 2034
Data de inscrição : 26/03/2015
Idade : 31
Localização : Brasil, Búzios.
Tópicos semelhantes» Fuvest 2006 - razão entre área do triângulo e área do círculo circunscrito
» A área do passeio representa a seguinte porcentagem da área do lago
» Raio, área lateral e área total do cone.
» Área lateral, área total e volume da pirâmede
» (F.C.M. STA. CASA - 1981) Área do Triângulo com a Área do círculo
» A área do passeio representa a seguinte porcentagem da área do lago
» Raio, área lateral e área total do cone.
» Área lateral, área total e volume da pirâmede
» (F.C.M. STA. CASA - 1981) Área do Triângulo com a Área do círculo
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
